If you are an IB Math AA or AI student, you have likely spent hours memorizing the Quadratic Formula. It’s a powerful tool, but sometimes you don't actually need to find the specific value of x . Sometimes, the question only asks: "How many solutions does this equation have?" or "Find the value of k for which this equation has distinct real roots."
This is where the discriminant comes into play. It is the "early warning system" of quadratics. By analyzing a small part of the formula, you can predict the behavior of the graph without solving the entire equation. At Easy Sevens Education, we often see students lose easy marks not because they don't know the formula, but because they stumble on the inequalities that follow. This guide will walk you through the logic, the method, and the common traps.
The Logic Behind the Discriminant
To understand the discriminant, look at the standard Quadratic Formula used to solve ax^2 + bx + c = 0 :
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
The discriminant is simply the expression underneath the square root symbol (the radicand). We denote it with the Greek letter Delta ( \Delta ).
\Delta = b^2 - 4ac
In the real number system, you cannot take the square root of a negative number. This mathematical rule dictates the "nature of roots" (the number and type of solutions) based entirely on whether that value is positive, zero, or negative.
Summary of Conditions: The Nature of Roots
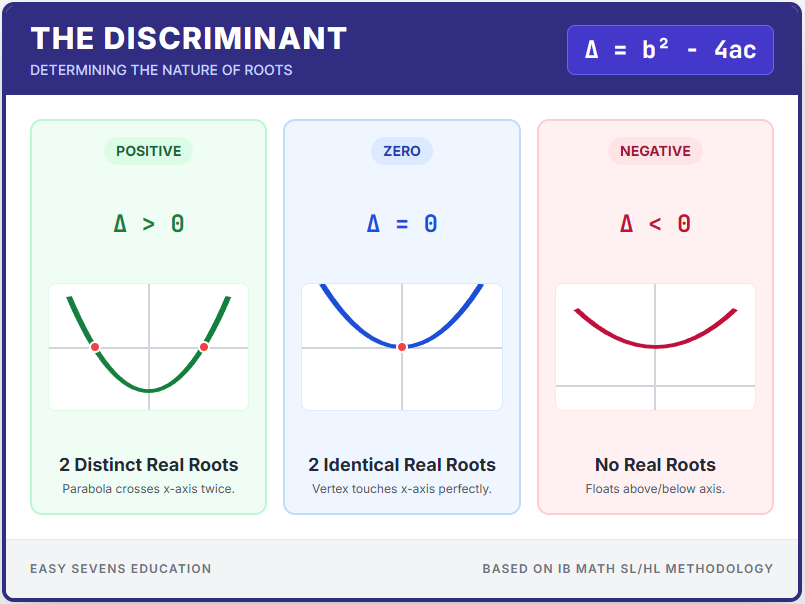
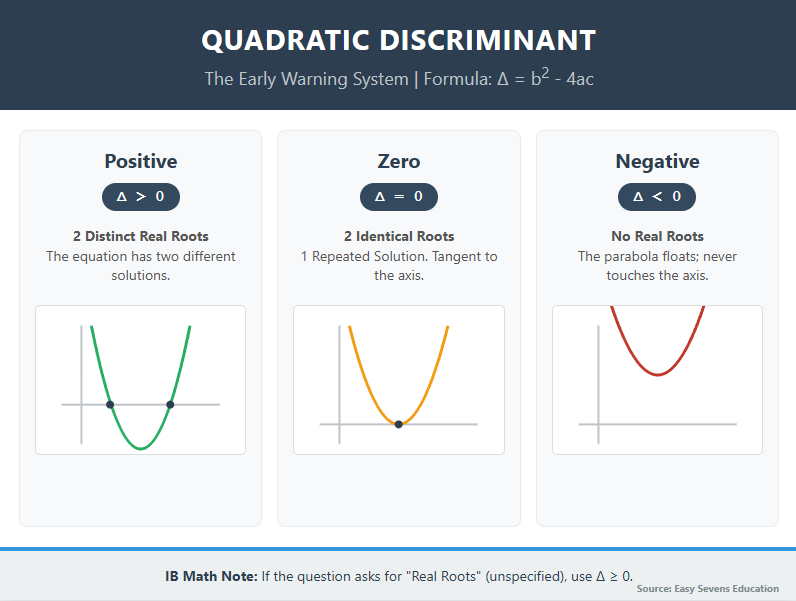
When an exam question asks for the "nature of roots," it is asking you to classify the quadratic into one of three categories. Here is how the value of \Delta changes the outcome.
| Discriminant Value | Nature of Roots | Graph Visualization |
|---|---|---|
| \Delta > 0 (Positive) | 2 Distinct Real Roots The equation has two different solutions. | The parabola crosses the x-axis at two separate points. |
| \Delta = 0 (Zero) | 2 Identical Real Roots (Often called 1 repeated solution). | The vertex of the parabola touches the x-axis perfectly (tangent). |
| \Delta < 0 (Negative) | No Real Roots The solutions are complex/imaginary. | The parabola floats above or below the x-axis and never touches it. |
A Note on Terminology
In IB Math, wording is precise. If a question says "Two identical real roots," it implies there is physically only one x-intercept, but mathematically, the factor appears twice (e.g., (x-3)(x-3)=0 ). The discriminant is exactly zero.
If the question simply says "Has real roots" (without specifying distinct or identical), you must use the condition: \Delta \ge 0 .
The "Finding k" Problem: A Step-by-Step Guide
The most common application of this concept in exams involves finding an unknown constant, usually labeled k , within the quadratic equation. This often leads to quadratic inequalities, which is where many students make algebraic errors.
Example Scenario
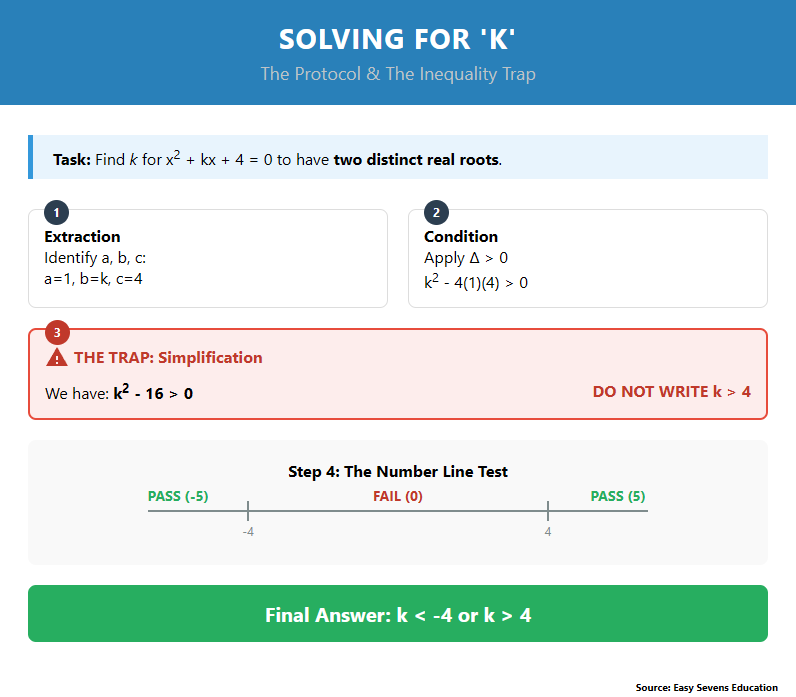
Find the values of k for which the equation x^2 + kx + 4 = 0 has two distinct real roots.
Step 1: Identify a, b, and c
First, extract the coefficients from the equation.
- a = 1
- b = k
- c = 4
Step 2: Set the Discriminant Condition
Since the question asks for "two distinct real roots," we know the discriminant must be strictly greater than zero.
b^2 - 4ac > 0
Step 3: Substitute and Simplify
Plug your values into the inequality:
(k)^2 - 4(1)(4) > 0
k^2 - 16 > 0
Step 4: Solve the Quadratic Inequality (The Trap!)
This is the critical moment. Many students instinctively write k > 4 and move on. This is incorrect. Because you are dealing with a quadratic inequality, you must consider both positive and negative scenarios.
When you have k^2 > 16 , you are asking: "What numbers, when squared, result in a value bigger than 16?"
- Obviously, numbers bigger than 4 work (e.g., 5, 6).
- However, numbers smaller than -4 also work (e.g., -5 squared is 25).
Method: The Number Line Test
To ensure accuracy, especially with harder numbers, follow this process:
- Find the Critical Values: Pretend it is an equation ( k^2 = 16 ). The values are k = 4 and k = -4 .
- Draw a Number Line: Mark -4 and 4. This creates three regions.
- Test a Point in Each Region:
- Region 1 ( k < -4 ): Test -5. (-5)^2 - 16 = 9 . This is > 0 . (Pass)
- Region 2 (Between -4 and 4): Test 0. 0^2 - 16 = -16 . This is NOT > 0 . (Fail)
- Region 3 ( k > 4 ): Test 5. 5^2 - 16 = 9 . This is > 0 . (Pass)
Final Answer: k < -4 or k > 4 .
Pro Tip: Visualizing the graph helps. Since k^2 - 16 is a "U-shaped" parabola (positive coefficient), the parts "greater than zero" are the "arms" pointing outward. Therefore, the solution is on the outside of the critical values.
Related Resources
Mastering the discriminant is just the first step in conquering IB Math. To fully prepare for your exams, you need to be comfortable with functions, calculus, and advanced algebra. At Easy Sevens Education, our IB math tutors have curated notes to help you connect these topics.
- For a deeper dive into the graphical implications of the discriminant, read our specific guide on the Number of Roots of a Quadratic.
- Aiming for the highest score possible? Don't miss our article on IB Math AA SL Level 7 Secrets.
- If you are struggling to apply these concepts in exam conditions, consider working with an expert. Learn more about our IB Math Tutoring Services.
Frequently Asked Questions
What if the coefficient 'a' contains k?
If your quadratic looks like kx^2 + 4x + 2 = 0 , your ‘a’ value is k . You proceed with the discriminant formula as usual: 4^2 – 4(k)(2) . However, you must add one extra condition: k \neq 0 . If k were 0, the x^2 term would vanish, and it would no longer be a quadratic equation.
Does "No Real Roots" mean there are no solutions at all?
Not quite. It means there are no <em>real</em> solutions. The parabola does not touch the x-axis. However, in advanced mathematics (and IB Math AA HL), we explore complex numbers, where we can find solutions involving imaginary units ( i ). For the purpose of the discriminant inequality in SL, you treat it as \Delta < 0 .
Why do I need to flip the inequality sign sometimes?
You only flip the inequality sign (e.g., changing > to < ) when you multiply or divide the entire inequality by a negative number. This often happens when solving for k if the k^2 term is negative (e.g., -4k^2 + 16 > 0 ). Always be careful with your negatives!
Can I use the discriminant for cubic equations?
What does "repeated root" mean geometrically?
Geometrically, a repeated root means the vertex of the parabola is sitting exactly on the x-axis. It is tangent to the axis. This occurs when the quadratic is a perfect square, such as (x-2)^2 = 0 .
Conclusion
The discriminant is a small formula with massive implications. Whether you are checking for distinct real roots, identical roots, or no real solutions, b^2 - 4ac is your key to unlocking the problem. Remember, the algebra doesn't end when you set up the inequality—be vigilant with your number lines and test points to ensure you capture every valid solution for k .
If you are finding quadratic inequalities tricky or want to ensure you are maximizing your marks in IB Math, we are here to help. Contact Easy Sevens Education today to find a tutor who can turn these concepts into easy sevens.