If you are an IB Math AA HL student, the non-calculator paper (Paper 1) likely gives you anxiety. You’ve switched from AI or standard math where the calculator was your best friend, and now you’re staring at a question asking for the exact value of Unit Circle angles like cosine of 7 pi over 6.
You have two choices: rote memorization of a terrifying diagram with 16 different coordinates, or learning the logic that makes it impossible to forget. At Easy Sevens Education, we believe in the latter. This guide is your cheat sheet to mastering the Unit Circle without the headache, using simple finger rules and logical patterns.
Why the Unit Circle Matters for IB Math AA HL
In the IB Math Analysis and Approaches (AA) Higher Level course, you cannot rely on your GDC for everything. Paper 1 requires strong mental math and algebraic manipulation. If you are asked to find the sine of 30 degrees or convert radians to degrees, you need the answer in seconds, not minutes.
Many students struggle because they treat trigonometry as a memory test. They fail to realize that the Unit Circle is just a graph. As discussed in our tutoring sessions:
- It is a graph with a radius of 1.
- Cosine is the X-coordinate (horizontal distance).
- Sine is the Y-coordinate (vertical distance).
Once you understand that you are simply finding (x, y) coordinates on a circle, the panic disappears.
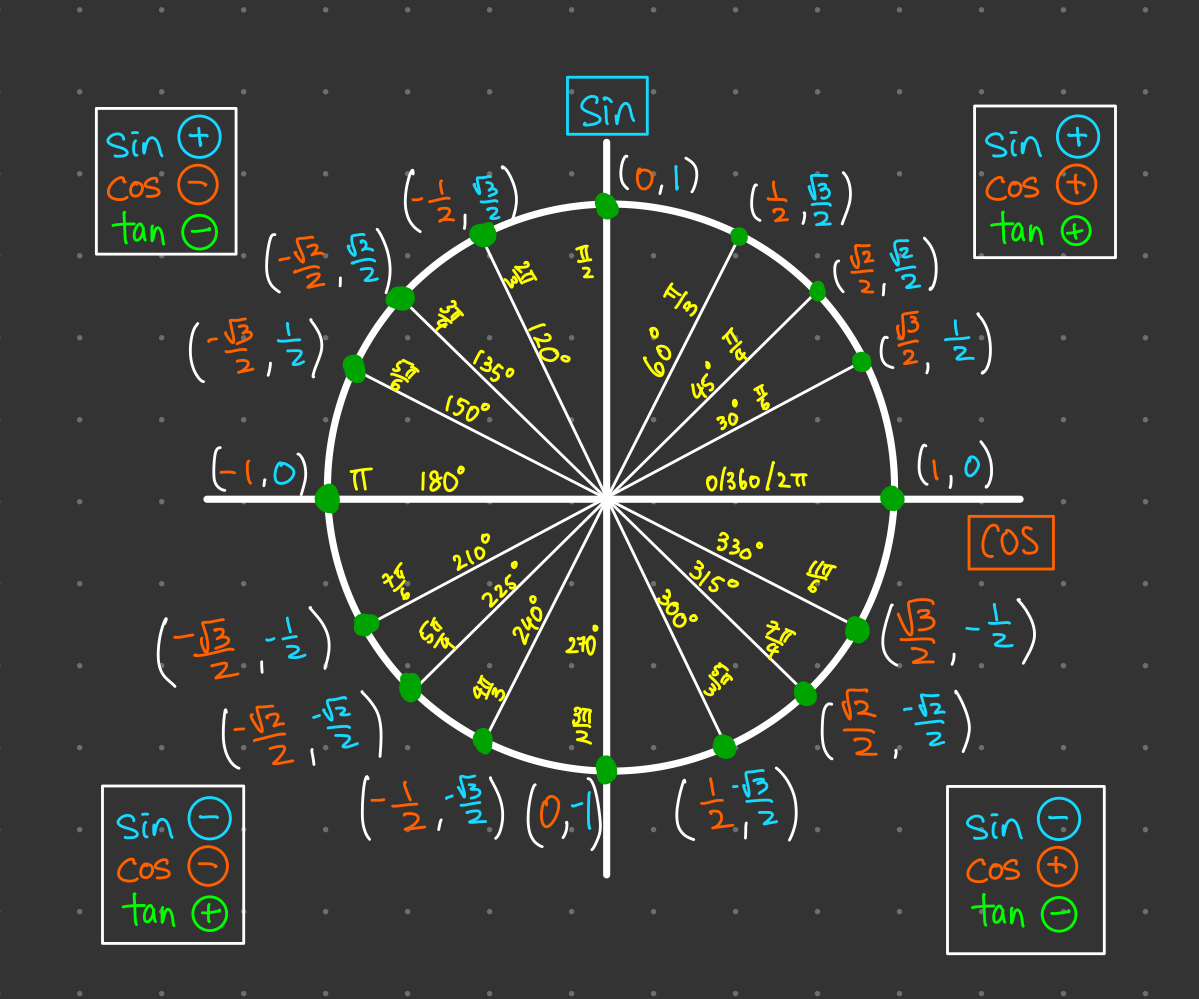
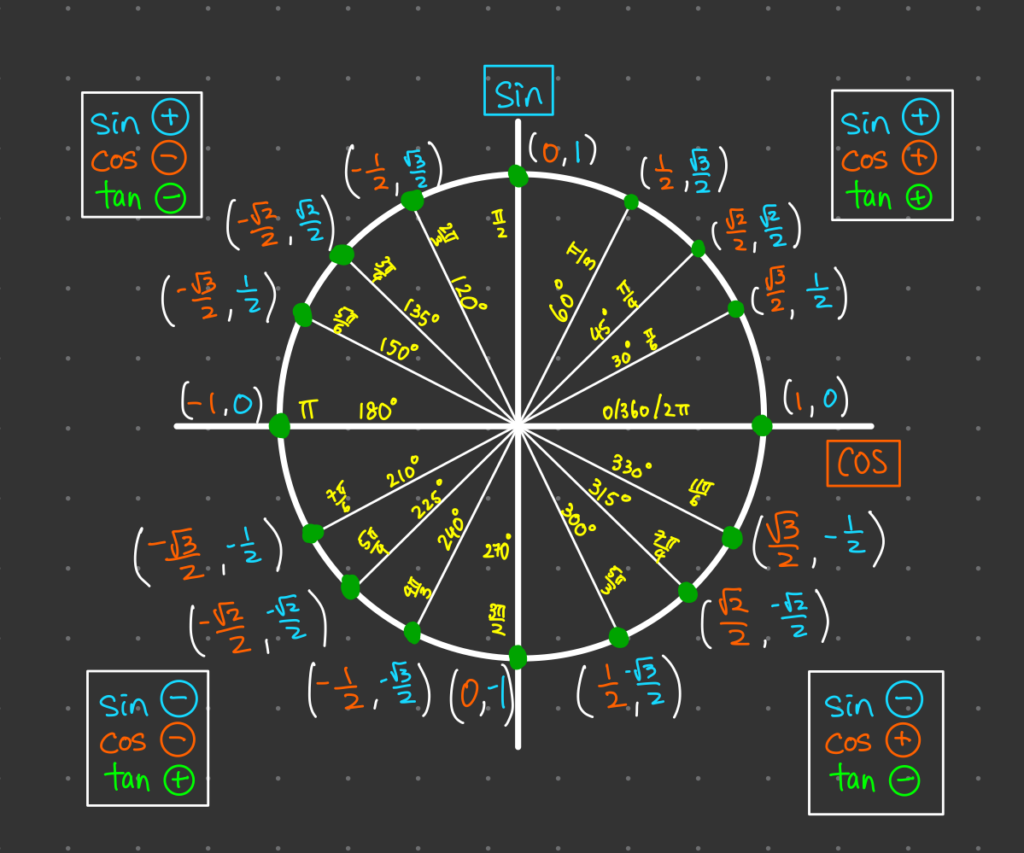
Unit Circle Reference Table: The First Quadrant
You do not need to memorize the entire circle. You only need to know the first quadrant (0 to 90 degrees). Everything else is just a mirror image. Here is the core data you need to lock in.
| Angle (Degrees) | Angle (Radians) | Coordinate (x, y) | Value (Cos, Sin) |
|---|---|---|---|
| 0° | 0 | (1, 0) | Cos = 1, Sin = 0 |
| 30° | \frac{\pi}{6} | (\frac{\sqrt{3}}{2}, \frac{1}{2}) | Cos = \frac{\sqrt{3}}{2} |
| 45° | \frac{\pi}{4} | (\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}) | Equal Values |
| 60° | \frac{\pi}{3} | (\frac{1}{2}, \frac{\sqrt{3}}{2}) | Sin = \frac{\sqrt{3}}{2} |
| 90° | \frac{\pi}{2} | (0, 1) | Cos = 0, Sin = 1 |
Unit Circle Graph
Understanding the Geometry: Finding the Angle θ
To use the Unit Circle effectively, you must understand how we define the angle \theta. In IB Math, we don’t just pick any angle inside the circle; we follow a specific geometric convention called “standard position.”
Terminal and Initial Arm of the Unit Circle
Every angle on the unit circle is formed by two rays meeting at the origin (0,0):
- The Initial Arm: This is the fixed ray that lies along the positive x-axis. We always start counting from here.
- The Terminal Arm: This is the ray that rotates from the origin to a specific point on the circumference of the circle. The position where this ray “terminates” determines the angle.
The angle \theta is defined as the measure of rotation from the positive x-axis to the terminal arm.
Direction of Rotation
You must be careful with the direction of your terminal arm:
- Counter-Clockwise (Positive): If the terminal arm rotates upwards from the x-axis, the angle is positive (e.g., +30^\circ).
- Clockwise (Negative): If the terminal arm rotates downwards, the angle is negative (e.g., -30^\circ).
Calculating θ from Coordinates
If you are given a point (x, y) on the circumference where the terminal arm ends, you can find the angle using the following relationships:
\cos(\theta) = x
\sin(\theta) = y
\tan(\theta) = \frac{y}{x}
For example, if the terminal arm lands on a point where the horizontal distance is \frac{1}{2} and the vertical distance is \frac{\sqrt{3}}{2}, you can work backward using your finger rules to identify that \theta must be 60^\circ (or \frac{\pi}{3} radians).
Unit Circle Math Tricks to Solve Without a Calculator
You don’t need to carry a reference sheet into the exam. You have one attached to your wrist. Here are the two most powerful mental models for solving trigonometry exact values.
1. The Left-Hand Finger Trick
This is the fastest way to find values for 0, 30, 45, 60, and 90 degrees. Hold up your left hand with your palm facing you.
- Pinky: 0°
- Ring Finger: 30°
- Middle Finger: 45°
- Index Finger: 60°
- Thumb: 90°
The Formula:
\text{Value} = \frac{\sqrt{\text{Fingers}}}{2}
How to use it:
- Bend the finger corresponding to the angle you want.
- For Cosine (x-value): Count the fingers above the bent finger (towards the thumb). Square root that number and divide by 2.
- For Sine (y-value): Count the fingers below the bent finger (towards the pinky). Square root that number and divide by 2.
Example: Cosine 30°
Bend your Ring Finger (30°).
Fingers above (Thumb, Index, Middle) = 3.
Result: \frac{\sqrt{3}}{2} .
2. The ASTC Rule (Logic for +/- Signs)
Once you know the value from the first quadrant, you need to determine if it is positive or negative based on where the angle lands. We use the mnemonic ASTC.
- A (Quadrant 1): All functions are positive.
- S (Quadrant 2): Sine is positive (because Y is positive). Others are negative.
- T (Quadrant 3): Tangent is positive (because negative divided by negative is positive).
- C (Quadrant 4): Cosine is positive (because X is positive).
Example: Sine 210°
210° is in the 3rd Quadrant (past 180°). The reference angle is 30°.
Value for Sine 30° = 0.5.
In Quadrant 3 (T), Sine is negative.
Answer: -0.5
Related Resources
Mastering the Unit Circle is just the first step in conquering IB Math AA HL. To truly succeed, you need to apply these concepts to complex functions and calculus problems. At Easy Sevens Education, we specialize in helping students bridge the gap between basic understanding and exam performance. If you are struggling with the transition from SL to HL or need help speeding up your mental math for Paper 1, our resources are designed for you.
Check out our comprehensive guides and tutoring options at Easy Sevens Education to see how we can support your journey to a 7.
Key Takeaways for the Unit Circle
The Unit Circle doesn’t have to be a source of stress. By shifting your focus from rote memorization to logic—using coordinates, the finger trick, and the ASTC rule—you can solve any trigonometric problem the IB throws at you. Remember, the goal isn’t just to pass; it’s to build a foundation that makes the harder calculus topics easier.
If you found this guide helpful and want to take your math skills to the next level, contact Easy Sevens Education today for personalized coaching and advanced study strategies.
Frequently Asked Questions (FAQ)
Do I need to memorize the entire Unit Circle?
No. You only need to memorize the first quadrant (0 to 90 degrees). For any angle larger than 90 degrees, you use “reference angles” to map it back to the first quadrant and then use the ASTC rule to determine if the value is positive or negative.
How do I convert degrees to radians quickly?
Remember that 180^\circ = \pi radians. To convert any degree to radians, multiply by \frac{\pi}{180}. For example, 30^\circ \times \frac{\pi}{180} = \frac{30\pi}{180} = \frac{\pi}{6}. Memorizing the special angles (30, 45, 60) makes this automatic over time.
Why is there no calculator allowed in Paper 1?
The IB wants to test your algebraic intuition and understanding of mathematical properties. If you rely on a calculator, you might get the answer 0.866 for Cosine 30, but the exam mark scheme requires the exact value \frac{\sqrt{3}}{2}. The Unit Circle ensures you get these exact values.
What is the hardest part of the Unit Circle for students?
Most students struggle with the negative signs. They correctly identify that the reference angle is 60 degrees, but forget that in the 4th quadrant, Sine is negative. Always write “ASTC” on your paper at the start of the exam to remind yourself.
How often should I practice Unit Circle questions?
In our tutoring programs, we recommend doing at least 10 practice questions a day until it becomes second nature. Speed is key for the IB Math AA HL exam, and you cannot afford to waste 2 minutes figuring out a simple sine value.