If you are an IB Math AA HL student, you have likely looked at a Mathematical Induction problem and felt a moment of panic. The notation looks complex, and the logic of proving a statement for an infinite set of integers can feel abstract.
However, here is the truth that many students miss: IB Math AA HL Mathematical Induction is actually one of the most reliable ways to score high marks on your exam. Unlike complex vectors or probability questions where the method changes based on the context, induction follows a rigid, algorithmic structure. It is essentially a recipe.
In this guide, we will break down the exact 4-step process you need to follow. If you memorize this structure and avoid one specific “trap” regarding the conclusion statement, you can turn these questions into guaranteed points.
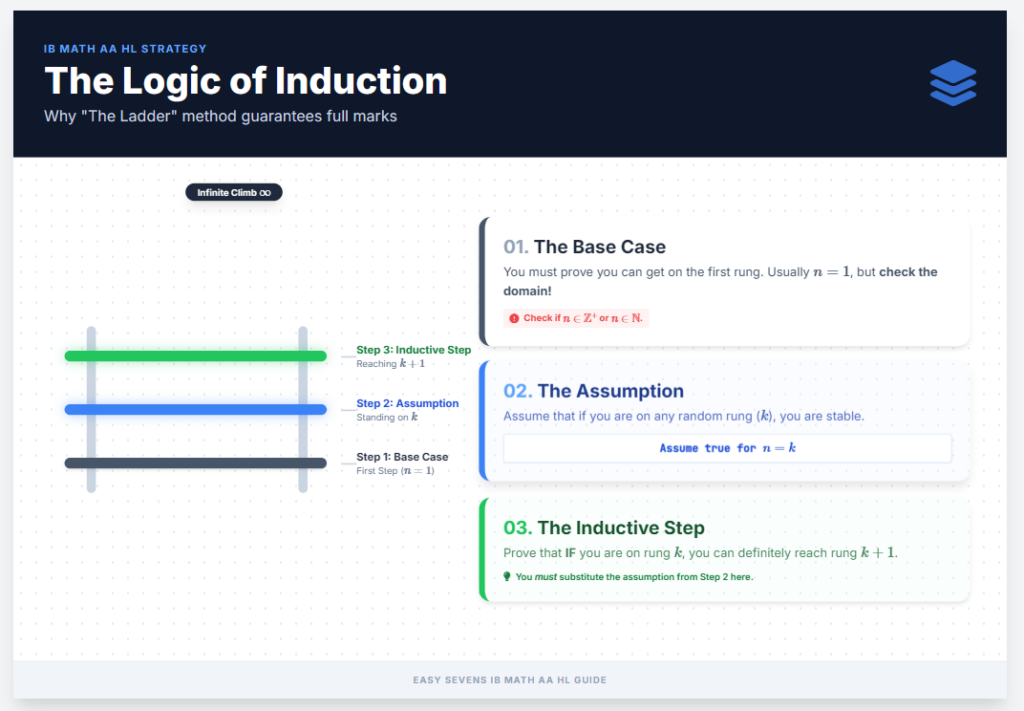
The “Ladder” Logic: Why Induction Works
Before we dive into the algebra, it is helpful to understand the logic. Think of mathematical induction like climbing a ladder:
- The Base Case: You must prove you can get on the first rung of the ladder (usually n=1).
- The Assumption: You assume that if you are on any random rung (k), you are stable.
- The Inductive Step: You prove that if you are on rung k, you can definitely reach rung k+1.
- The Conclusion: Since you can get on the first rung, and you can always move to the next one, you can climb the ladder forever.
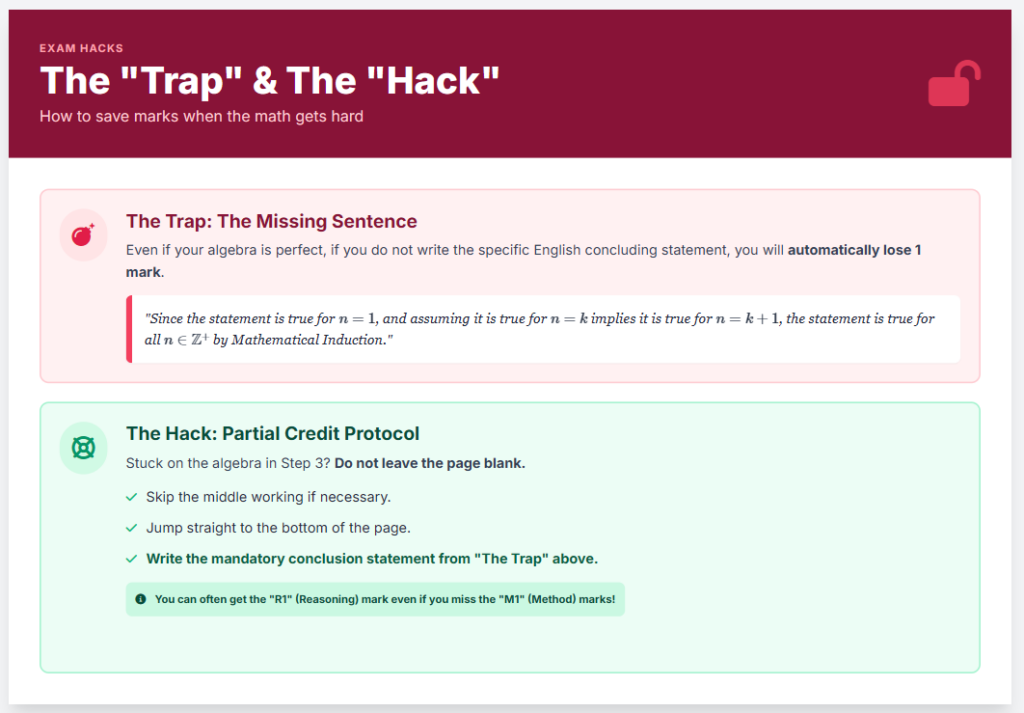
- The “Trap”: In the IB, even if you do all the math correctly, you will lose a mark if you do not write the specific English concluding statement. We will cover this in Step 4.
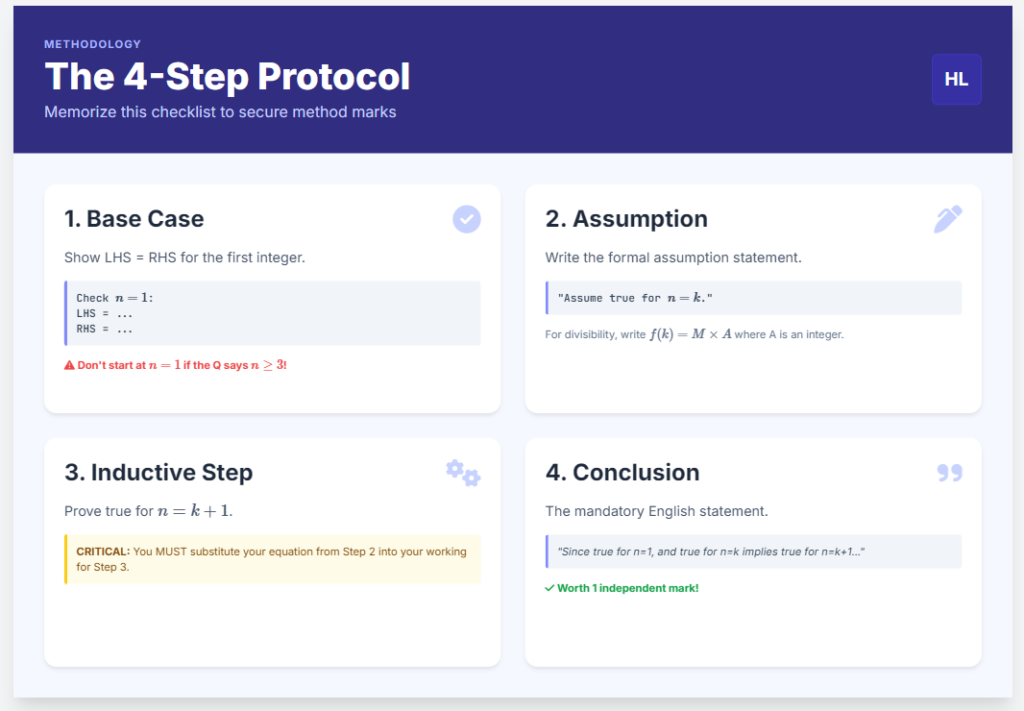
Quick Summary: The 4-Step Protocol
Here is a snapshot of what is required for every induction question. This structure applies whether you are proving divisibility, summation, or inequalities.
| Step Name | Action Required | Common Pitfall |
|---|---|---|
| 1. Base Case | Check if the statement is true for the first integer (usually n=1 or n=0). | Starting at the wrong number (e.g., using n=1 when the question asks for n \geq 3). |
| 2. Assumption | Write “Assume true for n=k.” | Forgetting to state this assumption clearly. |
| 3. Inductive Step | Prove true for n=k+1 using the assumption from Step 2. | Failing to substitute the n=k expression into the algebra. |
| 4. Conclusion | Write the mandatory formalized English statement. | Skipping this sentence results in an automatic deduction of 1 mark. |
Step-by-Step Walkthrough: A Divisibility Proof
Let’s solve a classic IB HL exam-style question together.
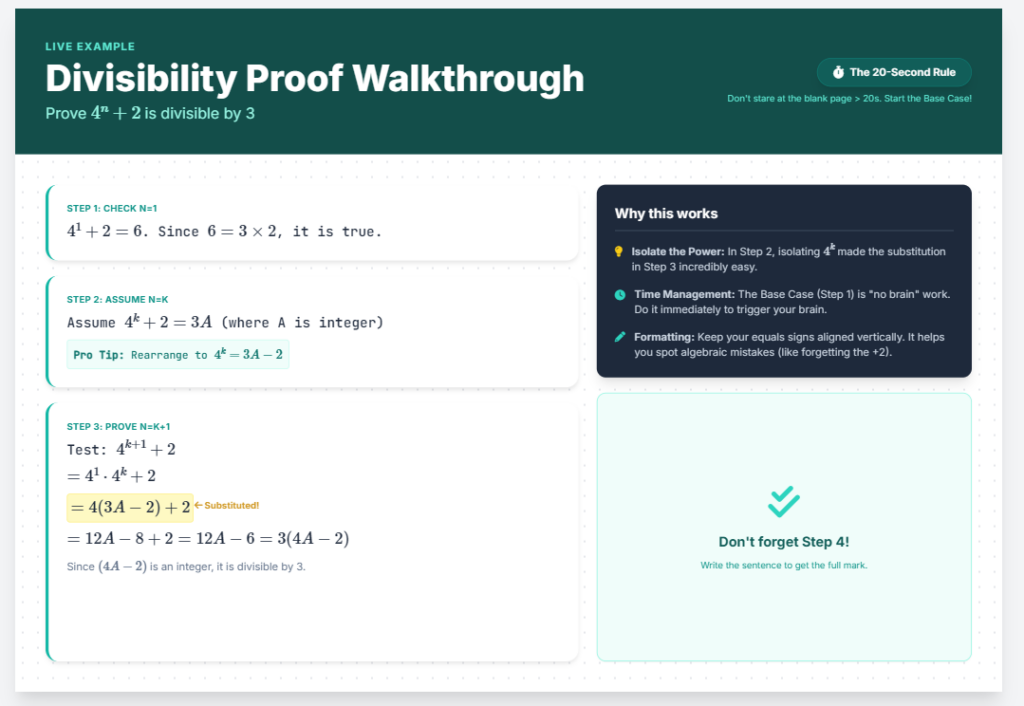
Prove that 4^n + 2 is divisible by 3 for all integers n \in \mathbb{Z}^+ .
Step 1: The Base Case (Check n = 1)
First, we need to show the statement holds for the starting value. Since the question specifies positive integers (\mathbb{Z}^+), we start at n=1.
Substitute n=1 into the expression:
4^{(1)} + 2 = 6
Since 6 is divisible by 3 (6 = 3 \times 2), the statement is true for n=1.
Step 2: The Assumption (n = k)
We assume the statement is true for a general integer k. In divisibility questions, this means we can rewrite the expression as a multiple of the divisor.
Write this down clearly:
“Assume true for n=k. Therefore, assume 4^k + 2 = 3A where A is an integer.”
Rearranging this to isolate the power term is a pro-tip that makes the next step easier:
4^k = 3A – 2
Step 3: The Inductive Step (Check n = k + 1)
Now, we must prove the statement is true for n=k+1. We start by substituting k+1 into our expression.
\text{Test: } 4^{(k+1)} + 2
Using exponent laws, we separate the +1:
= 4^1 \times 4^k + 2
= 4(4^k) + 2
Here is the key moment: You must substitute your assumption from Step 2 (4^k = 3A – 2) into this new equation. Without this substitution, the proof fails.
= 4(3A – 2) + 2
Now, expand and simplify:
= 12A – 8 + 2
= 12A – 6
To prove this is divisible by 3, factor out the 3:
= 3(4A – 2)
Since A is an integer, (4A – 2) is also an integer. Therefore, the expression is a multiple of 3. Thus, it is true for n=k+1.
Step 4: The Mandatory Conclusion
You have done the math, but you are not done yet. The IB requires a specific logical statement to tie everything together. If you skip this, you lose the final mark. Memorize this format:
“Since the statement is true for n=1, and assuming it is true for n=k implies it is true for n=k+1, the statement is true for all n \in \mathbb{Z}^+ by Mathematical Induction.”
Exam Tips from the Tutor
- Time Management: Do not spend more than 20 seconds staring at the blank page. Start the base case immediately. It triggers your brain to move to the next step.
- Partial Credit: If you get stuck on the algebra in Step 3, write the Step 4 conclusion anyway. You can sometimes still get the independent mark for the concluding statement even if the middle working is incomplete.
- Know Your Start Point: Always check if n is an “integer” (usually starts at 0 or 1) or a “positive integer” (starts at 1).
Related Resources
Mathematical Induction is just one tool in your HL toolkit. To excel in other challenging areas of the syllabus, review our guides on foundational concepts. Understanding the reasoning is crucial when induction is applied to sequences and series. Additionally, many induction proofs involve geometric applications, so ensuring your knowledge of Vectors is solid will help you spot patterns faster.
Conclusion
Mathematical Induction does not have to be the topic you dread. By treating it as a standardized 4-step process—Base Case, Assumption, Inductive Step, and Conclusion—you turn a complex proof into a checklist. Remember, the algebra might change, but the structure remains the same.
If you are struggling with HL concepts or want to improve your internal assessment, we are here to help clarify the complex.
Frequently Asked Questions
What if I can't finish the algebra in the exam?
If you cannot prove the Left Hand Side equals the Right Hand Side in step 3, do not erase your work. Skip to the end and write the mandatory English conclusion statement found in Step 4 of this guide. You will likely secure the “Reasoning” mark (R1) even if the “Method” marks (M1) were not fully achieved.
Does induction always start at n=1?
Not always. You must read the domain restriction given in the question. If the question says “for all integers n \geq 3,” your Base Case (Step 1) must be checking n=3, not n=1. If the question says n \in \mathbb{N}, check if your school defines Natural Numbers starting at 0 or 1.
Is this topic in Math AA SL?
No, Mathematical Induction is exclusively a Higher Level (HL) topic. It is typically found in Unit 1 (Number and Algebra), though some schools teach it later alongside Sequences and Series.
Why did I lose marks even though my math was correct?
The most common reason for losing marks on a perfect mathematical proof is missing the formalized conclusion. You must explicitly state that the truth of P(k) implies the truth of P(k+1) and link it back to the base case.