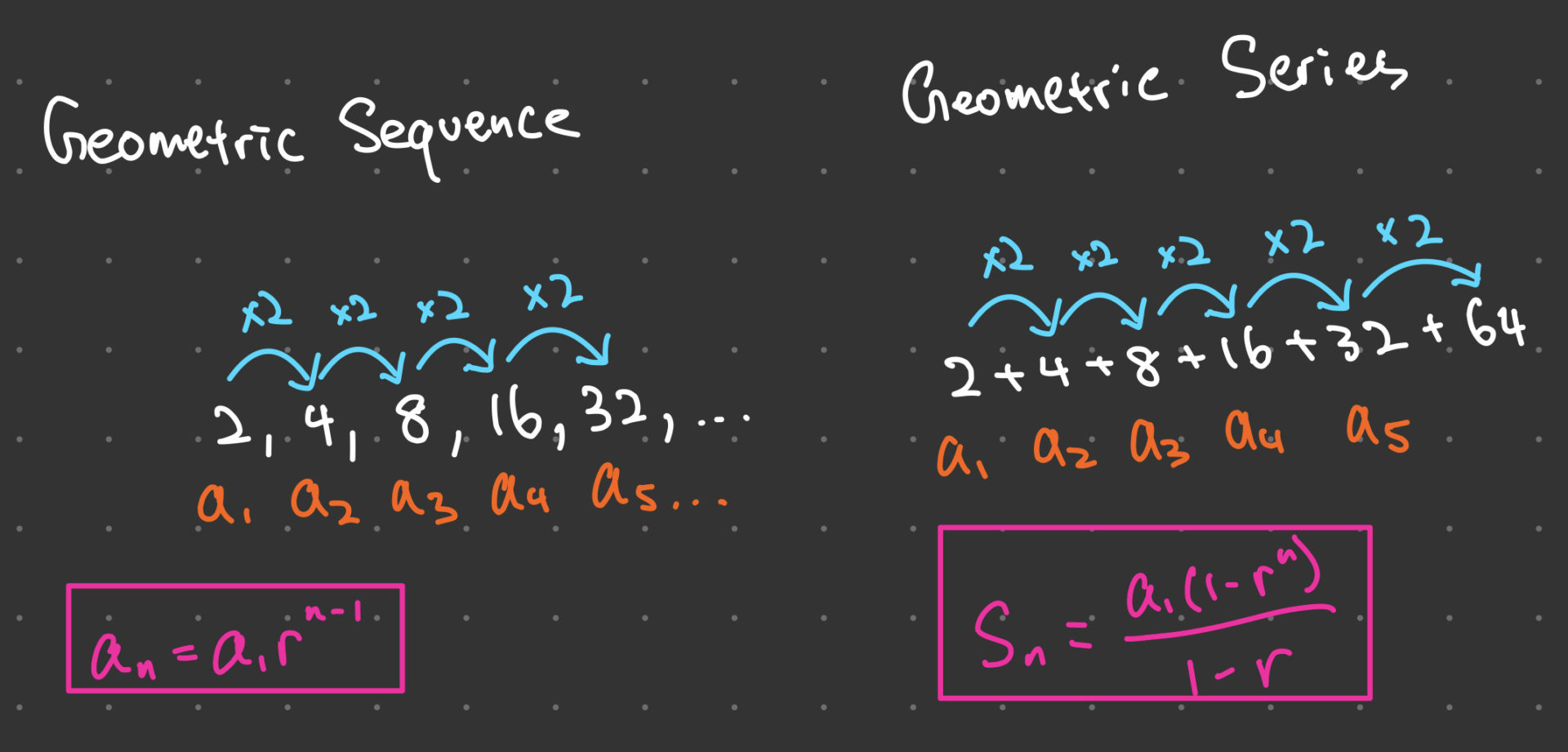Geometric sequences and series are an essential topic in the International Baccalaureate (IB) Math curriculum. Geometric sequences and series are a type of mathematical progression that involves multiplying a common ratio to the previous term. In this article, we will explore the concepts of geometric sequences and series, their applications, and solve some problems related to them. The examples used in this post are not the same as the examples used in the video. You should watch the video first to fully understand what geometric sequences and series are, and then read the following post to consolidate your understanding.
What Exactly is a Geometric Sequence?
Let’s start with the basics. A geometric sequence is an ordered list of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. Think of it as a pattern of multiplication.
Unlike an arithmetic sequence where you add a common difference, in a geometric sequence, you multiply by the common ratio (r). This simple difference leads to vastly different patterns of growth or decay – often much faster!
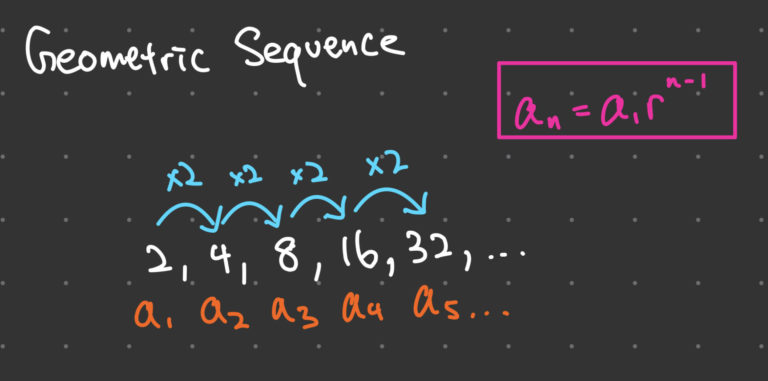
The Nth Term Geometric Sequence Formula
To find any term in a geometric sequence without having to list out every single one, we use a powerful formula. This is often called the geometric sequence formula or geometric progression formula.
The formula for the n-th term, denoted as a_n, of a geometric sequence is:
a_n = a_1 \cdot r^{n-1}
Let’s break down the variables:
a_n: This is the term you want to find (the n-th term).
a_1: This is the very first term in the sequence.
r: This is the common ratio. It’s the number you multiply by to get from one term to the next.
n: This is the position of the term you are trying to find (e.g., 1st, 2nd, 10th, etc.). The exponent n-1 indicates that you multiply by r one less time than the term number you’re looking for (since the first term a_1 is already given).
Finding the Common Ratio (r)
How do you figure out the common ratio r if you’re just given the sequence? It’s quite simple. You can find r by dividing any term by its preceding term.
The formula for the common ratio r is:
r = \frac{a_{n+1}}{a_n}
This means you can take the 2nd term divided by the 1st, or the 5th term divided by the 4th, and you should get the same value for r (as long as it is indeed a geometric sequence!).
Geometric Sequence Examples
Let’s look at some examples to solidify your understanding.
Example 1: Finding a specific term
Consider the sequence 5, 15, 45, 135, …
First, find the common ratio r. r = \frac{15}{5} = 3. We can check this: \frac{45}{15} = 3, \frac{135}{45} = 3. So, r=3.
The first term is a_1 = 5.
Let’s find the 7th term (n=7).
Using the formula a_n = a_1 \cdot r^{n-1}:
a_7 = 5 \cdot 3^{7-1}
a_7 = 5 \cdot 3^6
a_7 = 5 \cdot 729
a_7 = 3645
The 7th term of the sequence is 3645.
Example 2: Working with fractions
Consider the sequence 64, 32, 16, 8, …
Find the common ratio r. r = \frac{32}{64} = \frac{1}{2}. Checking: \frac{16}{32} = \frac{1}{2}, \frac{8}{16} = \frac{1}{2}. So, r = \frac{1}{2}.
The first term is a_1 = 64.
Let’s find the 5th term (n=5).
Using the formula a_n = a_1 \cdot r^{n-1}:
a_5 = 64 \cdot \left(\frac{1}{2}\right)^{5-1}
a_5 = 64 \cdot \left(\frac{1}{2}\right)^4
a_5 = 64 \cdot \frac{1}{16}
a_5 = \frac{64}{16}
a_5 = 4
The 5th term is 4. Notice how the terms are decreasing because the common ratio is between 0 and 1.
Geometric Sequences vs. Geometric Series: What’s the Difference?
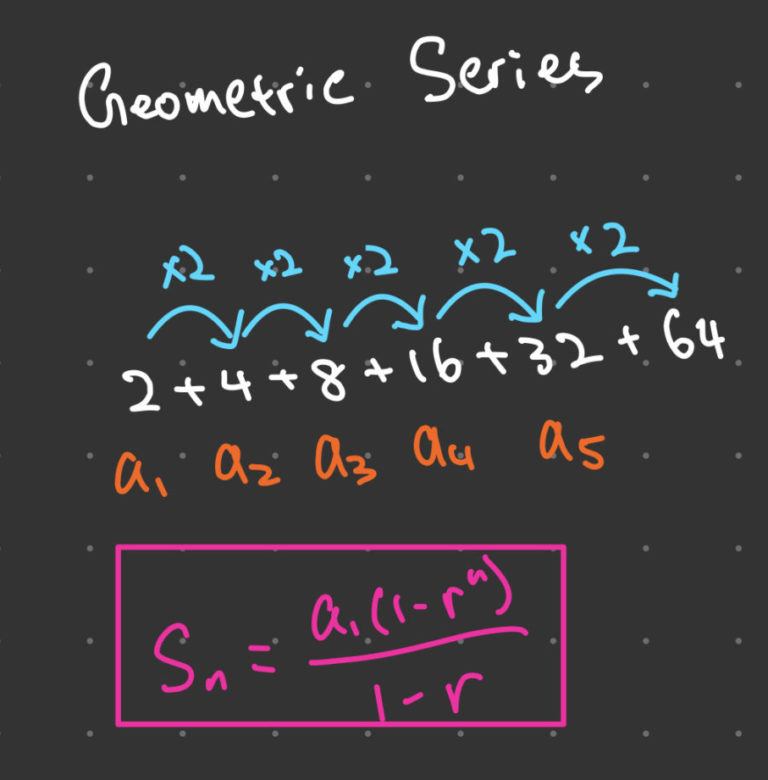
This is a common point of confusion! While they are closely related, a geometric sequence is the ordered list of terms, separated by commas (e.g., 2, 4, 8, 16). A geometric series is the sum of the terms in a geometric sequence (e.g., 2 + 4 + 8 + 16).
Think of a sequence as listing ingredients, and a series as mixing them all together to get a final dish!
Calculating the Sum: The Geometric Series Formula
Finding the sum of a geometric series, especially one with many terms, would be tedious if you had to add them all up manually. Luckily, there’s a formula for that too!
The Sum of the First N Terms (S_n)
The sum of the first n terms of a geometric series, denoted as S_n, is given by the formula:
S_n = \frac{a_1(1 – r^n)}{1 – r}
This formula is valid for any geometric series where the common ratio r \neq 1.
Let’s break down the parts of this formula:
S_n: This is the sum of the first n terms you want to find.
a_1: The first term of the sequence.
r: The common ratio.
n: The number of terms you are adding up.
What if r=1? If the common ratio is 1, the sequence is simply a_1, a_1, a_1, …. The sum of the first n terms is just n \cdot a_1.
Geometric Series Formula
Sum of Finite Geometric Series Examples
Let’s calculate the sum for a couple of examples.
Example 3: Sum with a positive ratio
Find the sum of the first 6 terms of the sequence 3, 6, 12, 24, …
First term a_1 = 3.
Common ratio r = \frac{6}{3} = 2.
Number of terms n = 6.
Using the formula S_n = \frac{a_1(1 – r^n)}{1 – r} :
S_6 = \frac{3(1 – 2^6)}{1 – 2}
S_6 = \frac{3(1 – 64)}{-1}
S_6 = \frac{3(-63)}{-1}
S_6 = \frac{-189}{-1}
S_6 = 189
The sum of the first 6 terms is 189.
Example 4: Sum with a negative ratio
Find the sum of the first 5 terms of the sequence 4, -12, 36, -108, …
First term a_1 = 4.
Common ratio r = \frac{-12}{4} = -3.
Number of terms n = 5.
Using the formula S_n = \frac{a_1(1 – r^n)}{1 – r} :
S_5 = \frac{4(1 – (-3)^5)}{1 – (-3)}
S_5 = \frac{4(1 – (-243))}{1 + 3}
S_5 = \frac{4(1 + 243)}{4}
S_5 = \frac{4(244)}{4}
S_5 = 244
The sum of the first 5 terms is 244. Notice how the terms alternate in sign, but the sum formula still works perfectly.
Diving into the Infinite: Infinite Geometric Series
Can you really add up an infinite number of terms and get a finite number? Surprisingly, sometimes you can! An infinite geometric series is the sum of all the terms in a geometric sequence that goes on forever.
a_1 + a_1 r + a_1 r^2 + a_1 r^3 + \dots
When Does an Infinite Sum Exist?
An infinite geometric series will only have a finite sum if the terms get progressively smaller and smaller, approaching zero. This happens when the absolute value of the common ratio r is less than 1.
The condition for convergence (meaning the sum exists) is:
|r| < 1
This means -1 < r < 1.
If |r| \ge 1, the terms either stay the same size or get larger, and their sum will grow infinitely large. In this case, the infinite series diverges, and the sum does not exist as a finite number.
The Infinite Sum Formula (S_\infty)
If the condition |r| < 1 is met, the sum of an infinite geometric series is given by the elegant formula:
S_\infty = \frac{a_1}{1 – r}
This formula is derived from the finite sum formula by observing that as n approaches infinity, r^n approaches 0 when |r| < 1. The formula \frac{a_1(1 – r^n)}{1 – r} then simplifies to \frac{a_1(1 – 0)}{1 – r} = \frac{a_1}{1 – r} .
Infinite Geometric Series Examples
Let’s see this formula in action.
Example 5: Converging infinite series
Find the sum of the infinite geometric series 10, 5, 2.5, 1.25, …
First term a_1 = 10.
Common ratio r = \frac{5}{10} = \frac{1}{2}.
Is |r| < 1? Yes, |\frac{1}{2}| = \frac{1}{2}, which is less than 1. The series converges.
Using the formula S_\infty = \frac{a_1}{1 – r} :
S_\infty = \frac{10}{1 – \frac{1}{2}}
S_\infty = \frac{10}{\frac{1}{2}}
S_\infty = 10 \cdot 2
S_\infty = 20
Even though there are infinite terms, their sum is exactly 20.
Example 6: Diverging infinite series
Consider the infinite geometric series 1, -2, 4, -8, …
First term a_1 = 1.
Common ratio r = \frac{-2}{1} = -2.
Is |r| < 1? No, |-2| = 2, which is not less than 1. The series diverges.
The sum of this infinite geometric series does not exist as a finite number. As you add more terms, the sum will oscillate between increasingly large positive and negative values.
Geometric Sequences & Series in Action: Real-World Applications
Geometric progressions aren’t just abstract mathematical concepts; they appear in many practical situations. Understanding them helps you model and predict various phenomena. Here are some common and interesting applications, particularly relevant for IB Math students:
Compound Interest (Financial Growth)
When you earn interest on your initial investment plus on the accumulated interest from previous periods, that’s compound interest. The value of your investment grows geometrically.
If you invest an amount P at an annual interest rate i (as a decimal), after one year, the amount is P(1+i). After two years, it’s P(1+i)^2, and so on.
The sequence of amounts at the end of each year (P(1+i), P(1+i)^2, P(1+i)^3, …) is a geometric sequence with first term a_1 = P(1+i) (or sometimes taken as P if the first term is the initial deposit before interest) and common ratio r = 1+i.
Population Growth (Biology/Ecology)
In conditions with abundant resources, populations (like bacteria or even humans in certain periods) can grow at a rate proportional to their current size. This can be modeled geometrically.
If a population N_0 grows by a factor of k each time period, the sequence of population sizes might look like N_0, N_0 k, N_0 k^2, N_0 k^3, ….
This is a geometric sequence with first term a_1 = N_0 and common ratio r = k.
Radioactive Decay (Physics)
Radioactive substances decay over time, with a fixed fraction of the substance breaking down in each unit of time (called the half-life). This is an example of a decreasing geometric sequence.
If a substance starts with mass M_0 and its half-life means half decays every 10 years, after 10 years, the mass is M_0 \cdot \frac{1}{2}. After 20 years (another half-life), it’s M_0 \cdot \frac{1}{2} \cdot \frac{1}{2} = M_0 \cdot (\frac{1}{2})^2, and so on.
The sequence of remaining mass after each half-life period (M_0, M_0 \cdot \frac{1}{2}, M_0 \cdot (\frac{1}{2})^2, …) is a geometric sequence with a_1 = M_0 and common ratio r = \frac{1}{2}. This is a converging sequence.
Damped Oscillations (Physics)
When a pendulum swings or a spring bounces, friction or air resistance causes the amplitude of each swing to decrease by a relatively constant percentage. The maximum displacement from equilibrium in successive swings forms a geometric sequence with a common ratio less than 1.
Medicine Dosage Accumulation (Biology/Medicine)
If a patient takes a regular dose of medicine, and the body eliminates a certain percentage of the drug between doses, the amount of medicine in the bloodstream right after each dose can be modeled using a geometric series (specifically, the sum of remaining portions of previous doses plus the new dose). Understanding the sum of this series is crucial for determining if the drug level reaches a steady, therapeutic amount.
Geometric Sequences vs. Arithmetic Sequences: A Quick Comparison
Since these are often taught together, it’s helpful to quickly contrast them.
Arithmetic Sequence: You add a constant value (the common difference, d) to get the next term. Formula for nth term: a_n = a_1 + (n-1)d.
Geometric Sequence: You multiply by a constant value (the common ratio, r) to get the next term. Formula for nth term: a_n = a_1 \cdot r^{n-1}.
Arithmetic sequences show linear growth (or decay), while geometric sequences demonstrate exponential growth (or decay).
Preparing for IB Math
Understanding geometric sequences and series is fundamental for several topics in the IB Math curriculum, including financial mathematics, probability (especially in repeated events), and calculus (when discussing series convergence). Practicing with various examples – finding terms, common ratios, finite sums, and analyzing infinite series – will build the intuition and skill needed for success in your exams and assignments.
Conclusion
Geometric sequences and series provide a powerful mathematical framework for understanding patterns of multiplicative change. From calculating compound interest and modeling population growth to analyzing radioactive decay and designing electrical circuits, these concepts have wide-ranging applications in the real world. By mastering the formulas for finding the nth term, the sum of a finite series, and the sum of an infinite series (when it converges), you gain valuable tools applicable across science, finance, and engineering. Keep practicing, explore different examples, and you’ll find these concepts becoming clear and intuitive, boosting your confidence in IB Math and beyond!
Frequently Asked Questions (FAQ)
A geometric sequence is a list of numbers where each term is found by multiplying the previous one by a common ratio (e.g., 2, 4, 8). A geometric series is the sum of the terms in a geometric sequence (e.g., 2 + 4 + 8).
Divide any term by its preceding term. The formula is r = \frac{a_{n+1}}{a_n} .
The formula is a_n = a_1 \cdot r^{n-1} , where a_n is the nth term, a_1 is the first term, and r is the common ratio.
The formula is S_n = \frac{a_1(1 – r^n)}{1 – r} , where S_n is the sum of the first n terms, a_1 is the first term, and r is the common ratio (r \neq 1).
An infinite geometric series has a finite sum only if the absolute value of its common ratio (r) is less than 1, i.e., |r| < 1 or -1 < r < 1.
If |r| < 1, the formula for the sum of an infinite geometric series is S_\infty = \frac{a_1}{1 – r} .
Compound interest is a great example. If you deposit money and earn a fixed percentage interest each year, the total amount of money in your account at the end of each year forms a geometric sequence.
In arithmetic sequences, you add a constant difference. In geometric sequences, you multiply by a constant ratio. This leads to linear growth in arithmetic sequences versus exponential growth (or decay) in geometric sequences.