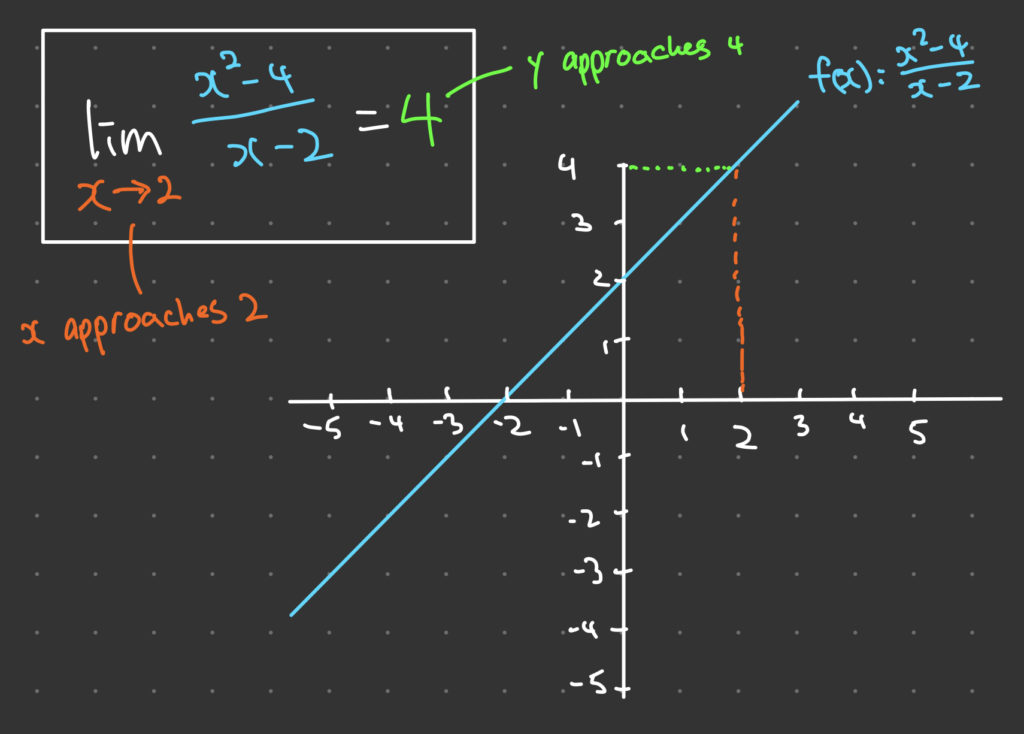Limits are a fundamental concept in calculus and are an essential tool for solving problems in various fields of mathematics, engineering, and science. They are used to describe the behavior of a function as its input values get closer and closer to a particular value, often referred to as the limit point. In this article, we will explore the basics of limits in IB Math, including the definition of limits, limit notation, types of limits, and how to evaluate limits. The examples used in this post are not the same as the examples used in the video. You should watch the video first to fully understand what limits are, and then read the following post to consolidate your understanding.
What is a Limit?
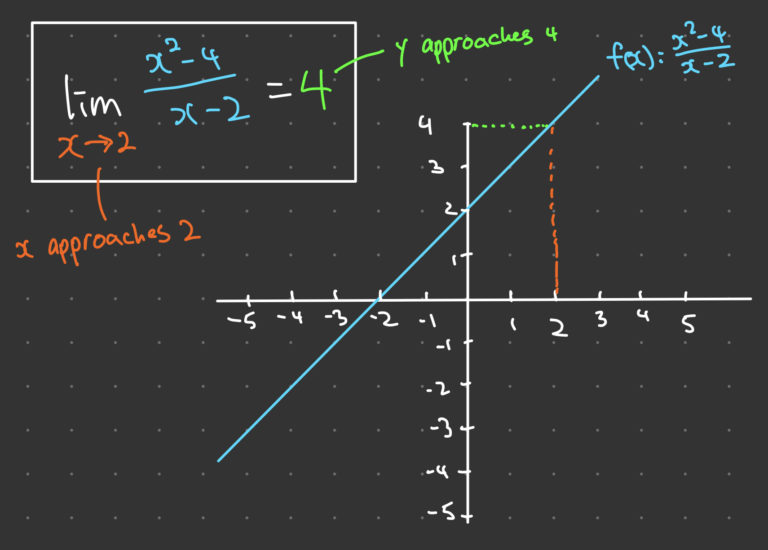
In mathematics, a limit is a fundamental concept used to describe the behavior of a function as its input values get closer and closer to a particular value. More specifically, a limit is the value that a function approaches as the input value approaches a particular value. This value may or may not be the same as the function value at the particular value.
For example, consider the function f(x)=\frac{x^2-4}{x-2} . The function is not defined at x=2 because the denominator is zero. However, we can find the limit of the function as x approaches 2. To find the limit, we need to evaluate the function as x gets closer and closer to 2, but never actually reaches 2. We can do this by substituting values of x that are close to 2 into the function and observing the values of the function as we get closer and closer to 2.
Limit Notation
There are different ways to express limits mathematically. The most common notation used to represent the limit of a function is as follows:
\lim_{x \to a} f(x) = L
This notation represents the limit of f(x) as x approaches a , and it equals L .
For example, the limit of f(x)=\frac{x^2-4}{x-2} as x approaches 2 can be written as:
\lim_{x \to 2} \frac{x^2-4}{x-2}
Types of Limits
There are three types of limits: finite limits, infinite limits, and limits at infinity.
Finite Limits
A finite limit is a limit where the function approaches a finite value as the input value approaches a particular value. In other words, the limit exists and is a real number.
For example, consider the function f(x)=\frac{x^2-4}{x-2} . The limit of the function as x approaches 2 is a finite limit because the function approaches a finite value (4) as x gets closer and closer to 2.
Infinite Limits
An infinite limit is a limit where the function approaches positive or negative infinity as the input value approaches a particular value. In other words, the limit does not exist, and the function value becomes infinitely large (or small) as the input value gets closer and closer to a particular value.
For example, consider the function g(x)=\frac{1}{x} . The limit of the function as x approaches 0 is an infinite limit because the function approaches infinity as x gets closer and closer to 0. We can write this limit as:
\lim_{x \to 0} \frac{1}{x} = \infty
Limits at Infinity
A limit at infinity is a limit where the input value approaches infinity or negative infinity, and the function approaches a finite value or infinity. In other words, the function value gets closer and closer to a particular value or infinity as the input value becomes infinitely large (or small).
For example, consider the function h(x)=\frac{3x+5}{2x-1} . The limit of the function as x approaches infinity is a limit at infinity because the function approaches a finite value ( \frac{3}{2}) as x becomes infinitely large. We can write this limit as:
\lim_{x \to \infty} \frac{3x+5}{2x-1} = \frac{3}{2}
How to Evaluate Limits
There are different methods to evaluate limits, including direct substitution, factoring, rationalization, and L’Hopital’s Rule.
Direct Substitution
Direct substitution is a method used to evaluate limits by substituting the limit point into the function and simplifying the expression. This method works when the function is continuous at the limit point.
For example, consider the function f(x)=\frac{x^2-4}{x-2} . To evaluate the limit of the function as x approaches 2, we can use direct substitution by substituting 2 into the function and simplifying the expression:
\lim_{x \to 2} \frac{x^2-4}{x-2} = \frac{2^2-4}{2-2} = \frac{0}{0}
The result of this expression is undefined, which means that we cannot evaluate the limit of the function using direct substitution.
Factoring
Factoring is a method used to evaluate limits by factoring the numerator and denominator of the function and simplifying the expression. This method works when the function is undefined at the limit point because of a removable discontinuity.
For example, consider the function g(x)=\frac{x^2-4}{x-2} . To evaluate the limit of the function as x approaches 2, we can use factoring by factoring the numerator as a difference of squares:
\lim_{x \to 2} \frac{x^2-4}{x-2} = \lim_{x \to 2} \frac{(x+2)(x-2)}{x-2}
We can simplify the expression by canceling out the common factor of (x-2):
\lim_{x \to 2} \frac{(x+2)(x-2)}{x-2} = \lim_{x \to 2} (x+2) = 4
The limit of the function as x approaches 2 is 4.
Rationalization
Rationalization is a method used to evaluate limits by multiplying the numerator and denominator of the function by a conjugate expression to eliminate radicals or complex numbers. This method works when the function contains radicals or complex numbers.
For example, consider the function h(x)=\frac{\sqrt{x+1}-1}{x} . To evaluate the limit of the function as x approaches 0, we can use rationalization by multiplying the numerator and denominator by the conjugate expression (\sqrt{x+1}+1) :
\lim_{x \to 0} \frac{\sqrt{x+1}-1}{x} = \lim_{x \to 0} \frac{(\sqrt{x+1}-1)(\sqrt{x+1}+1)}{x(\sqrt{x+1}+1)} = \lim_{x \to 0} \frac{x}{x(\sqrt{x+1}+1)} = \lim_{x \to 0} \frac{1}{\sqrt{x+1}+1} = \frac{1}{2}
The limit of the function as x approaches 0 is \frac{1}{2}.
L’Hopital’s Rule (HL Only)
L’Hopital’s Rule is a method used to evaluate limits of indeterminate forms, where the numerator and denominator of the function both approach zero or infinity. This method involves taking the derivative of the numerator and denominator of the function until the indeterminate form is resolved.
For example, consider the function f(x)=\frac{\ln(x+1)}{x} . To evaluate the limit of the function as x approaches 0, we can use L’Hopital’s Rule by taking the derivative of the numerator and denominator of the function:
\lim_{x \to 0} \frac{\ln(x+1)}{x} = \lim_{x \to 0} \frac{\frac{d}{dx}(\ln(x+1))}{\frac{d}{dx}(x)} = \lim_{x \to 0} \frac{\frac{1}{x+1}}{1} = 1
The limit of the function as x approaches 0 is 1.
Tips for Solving Limits
Solving limits can be challenging, but there are some tips that can help make the process easier:
- Simplify the expression by factoring, canceling, or rationalizing if possible.
- Look for common algebraic expressions or trigonometric identities that can be used to simplify the expression.
- Identify the type of limit (left-sided, right-sided, or at infinity) and use the appropriate method to evaluate the limit.
- Use L’Hopital’s Rule as a last resort if other methods do not work.
- Check your answer by graphing the function or using a table of values to confirm that the limit exists and is equal to your answer.
Conclusion
Limits are a fundamental concept in mathematics and are used in a wide range of fields, including calculus, physics, and engineering. Understanding the concept of limits is essential for solving complex mathematical problems and developing critical thinking skills. In this article, we have introduced the concept of limits, discussed the types of limits, and explained how to evaluate limits using various methods. By following the tips for solving limits, you can become proficient in solving even the most challenging limit problems.
FAQ
What is the definition of a limit in calculus?
A limit is the value that a function approaches as the input value approaches a particular value or infinity. A limit is defined as the mathematical concept of “closeness” between the function and the input value, and it is denoted using the symbol “lim”.
What is the difference between left-sided and right-sided limits?
Left-sided limits refer to the limit of a function as the input value approaches a particular value from the left side (i.e., values smaller than the particular value), while right-sided limits refer to the limit of a function as the input value approaches a particular value from the right side (i.e., values larger than the particular value). If the left-sided limit and right-sided limit are equal, the limit exists.
What is L’Hopital’s Rule?
L’Hopital’s Rule is a method used to evaluate limits of indeterminate forms, where the numerator and denominator of the function both approach zero or infinity. This method involves taking the derivative of the numerator and denominator of the function until the indeterminate form is resolved.
What are some tips for solving limits?
Some tips for solving limits include simplifying the expression by factoring, canceling, or rationalizing if possible, looking for common algebraic expressions or trigonometric identities that can be used to simplify the expression, identifying the type of limit and using the appropriate method to evaluate the limit, using L’Hopital’s Rule as a last resort if other methods do not work, and checking the answer by graphing the function or using a table of values.
What is the importance of limits in mathematics?
Limits are a fundamental concept in mathematics and are used in a wide range of fields, including calculus, physics, and engineering. Understanding the concept of limits is essential for solving complex mathematical problems and developing critical thinking skills. Limits are used to define continuity, derivatives, and integrals, which are essential concepts in calculus. Limits also play a crucial role in studying the behavior of functions and solving equations.