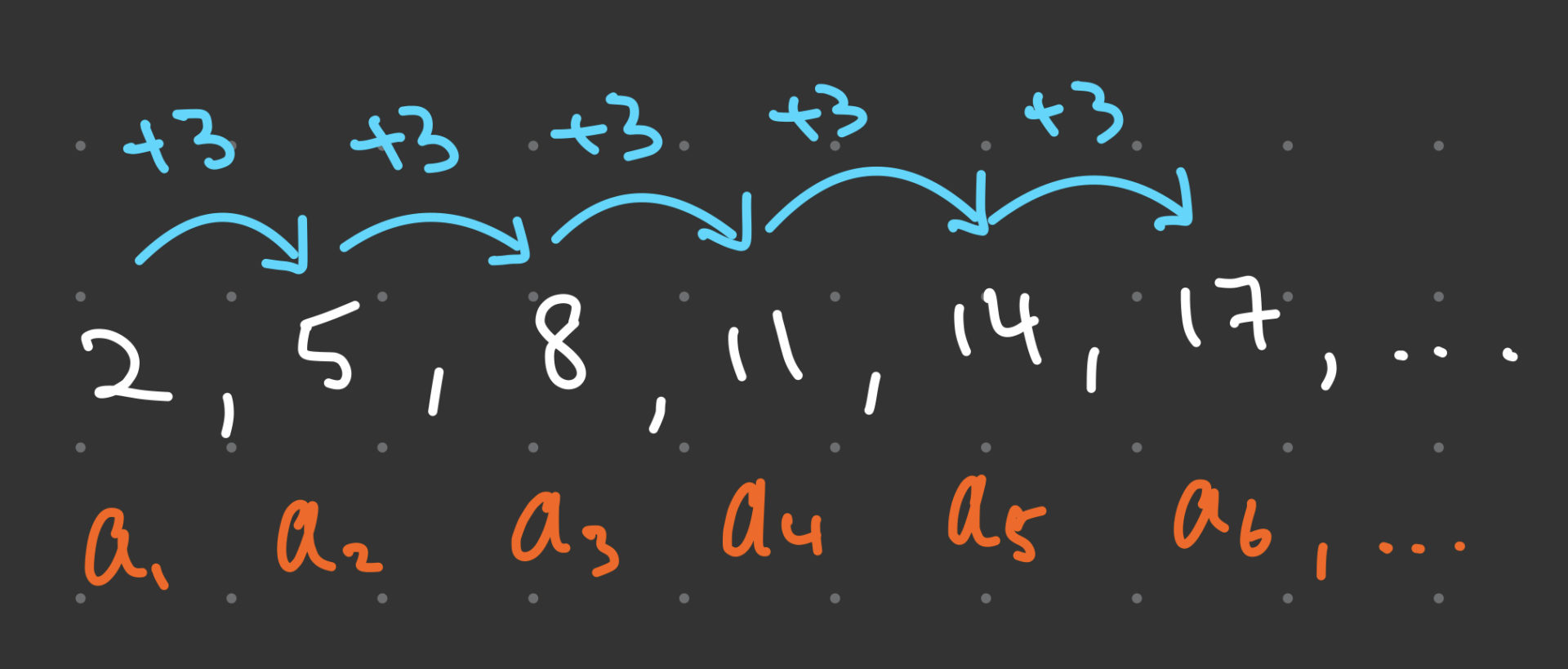As a student pursuing the International Baccalaureate (IB) diploma, one of the required courses is Mathematics. In this course, you will come across different topics, one of which is arithmetic sequences and series. The concepts of arithmetic sequence and series are fundamental in the study of mathematics, and they play a crucial role in various fields like physics, engineering, and finance.
In this blog post, we will delve into the topic of arithmetic sequence and series in detail, starting from the basics to the more complex aspects. We will also provide practical examples to help you understand these concepts better. The examples used below are different to the ones you see in the video above. You should first watch the video and refer to the information below to check your understanding.
What is an Arithmetic Sequence?
An arithmetic sequence is a sequence of numbers where each term is obtained by adding a constant value to the previous term. This constant value is also known as the common difference of the sequence.
For example, consider the sequence: 2, 5, 8, 11, 14, 17…
In this sequence, the first term is 2, and the common difference is 3. Therefore, to obtain the second term, we add 3 to 2, which gives 5. To get the third term, we add 3 to 5, which gives 8, and so on.
We can define an arithmetic sequence more formally as follows:
An arithmetic sequence is a sequence of numbers a1, a2, a3,…, an where the difference between any two consecutive terms is constant. In other words, a2 – a1 = a3 – a2 = a4 – a3 = … = d.
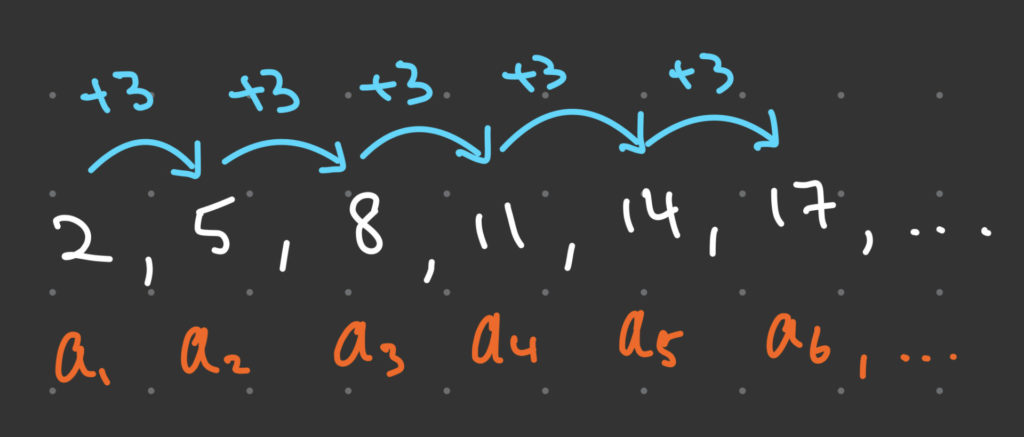
Finding the nth Term of an Arithmetic Sequence
Suppose we have an arithmetic sequence a1, a2, a3,…, an, with the first term a1 and common difference d. To find the nth term, we can use the following formula:
[nth term] = a_{n} = a_{1} + (n-1)d
For example, consider the arithmetic sequence 3, 6, 9, 12, 15,….
Here, the first term a1 is 3, and the common difference d is 3. To find the 10th term of the sequence, we can substitute n=10 in the formula above, which gives:
[10th term] = a_{10} = 3 + (10-1)3 = 30
Therefore, the 10th term of the sequence is 30.
Finding the Sum of an Arithmetic Series
An arithmetic series is the sum of the terms of an arithmetic sequence. To find the sum of the first n terms of an arithmetic sequence, we can use the following formula:
[sum of n terms] = S_{n} = \frac{n}{2}(a_{1} + a_{n})
For example, consider the arithmetic sequence 2, 5, 8, 11, 14,….
Here, the first term a1 is 2, the common difference d is 3, and we want to find the sum of the first 10 terms of the sequence.
Using the formula above, we can find the sum of the first 10 terms as follows:
[sum of 10 terms] = S_{10} = \frac{10}{2}(2 + a_{10})
We can find the value of a10 using the formula for the nth term, which gives:
[10th term] = a_{10} = 2 + (10-1)3 = 29
Substituting a10 = 29, we get:
[sum of 10 terms] = S_{10} = \frac{10}{2}(2 + 29) = 155
Therefore, the sum of the first 10 terms of the arithmetic sequence 2, 5, 8, 11, 14,… is 155.
Applications of Arithmetic Sequence and Series
Arithmetic sequences and series have various applications in real-life situations. Here are a few examples:
1. Financial Planning
Arithmetic sequences and series are used in financial planning to determine the amount of money needed for future investments, mortgages, or loans. For example, to calculate the monthly payments on a mortgage, we use the formula for the sum of an arithmetic series.
2. Physics and Engineering
Arithmetic sequences and series are used in physics and engineering to model physical phenomena, such as the motion of objects, changes in temperature, and electrical currents.
3. Sports
Arithmetic sequences and series are used in sports to keep track of scores and statistics. For example, the number of points scored by a basketball team over a season can be modeled using an arithmetic sequence.
Conclusion
Arithmetic sequence and series are an essential topic in mathematics that have various applications in real-life situations. We hope that this blog post has helped you understand the concepts of arithmetic sequence and series better. Remember, practice is crucial to mastering this topic, so make sure to solve plenty of problems and seek help when needed.
FAQ
Q1. What is the difference between an arithmetic sequence and a geometric sequence?
A1. In an arithmetic sequence, each term is obtained by adding a constant value to the previous term, whereas in a geometric sequence, each term is obtained by multiplying the previous term by a constant value.
Q2. Can an arithmetic series have a negative common difference?
A2. Yes, an arithmetic series can have a negative common difference. In this case, the sequence will be decreasing instead of increasing.
Q3. How do I find the common difference of an arithmetic sequence?
A3. To find the common difference of an arithmetic sequence, subtract any term from the previous term. The result will be the common difference.
Q4. Can the sum of an arithmetic series be negative?
A4. Yes, the sum of an arithmetic series can be negative if the terms of the sequence alternate between positive and negative values.
Q5. Can I use the formula for the sum of an arithmetic series to find the sum of an infinite arithmetic series?
A5. No, the formula for the sum of an arithmetic series only applies to finite series. To find the sum of an infinite arithmetic series, you need to use a different formula.