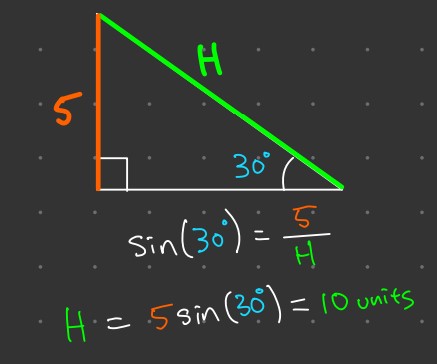IB Math: SOH-CAH-TOA | Meaning, Diagrams, and Examples

Today, we’re diving into a topic of IB Maths that might sound like a secret code: SOH CAH TOA. Don’t worry; it’s not a mysterious incantation but a powerful set of tools that will make trigonometry your new best friend.

Common Convention for Right Angle Triangle Notation

Before we dive into the world of primary trigonometric ratios, we first have to understand the common notations for right angled triangles. In the common notation for a right-angled triangle, angles are typically denoted using capital letters, such as A, B, and C. Corresponding side lengths are represented by lowercase letters, with a, b, and c commonly used. The convention ensures clarity in identifying the relationships between angles and their opposite sides. For instance, angle A corresponds to side a, angle B to side b, and angle C to side c. This consistent use of matching letters aids in understanding the geometric properties of the triangle, as the side opposite an angle shares the same letter designation. This notational system simplifies the communication of trigonometric concepts, facilitating a concise and standardized representation of right-angled triangles.

What is SOH CAH TOA?

SOH CAH TOA is not some ancient language but an acronym to remember three fundamental trigonometric ratios: Sine, Cosine, and Tangent. These ratios play a crucial role in solving triangles and understanding the relationships between their angles and sides.

Let’s break down the mystery behind each term:

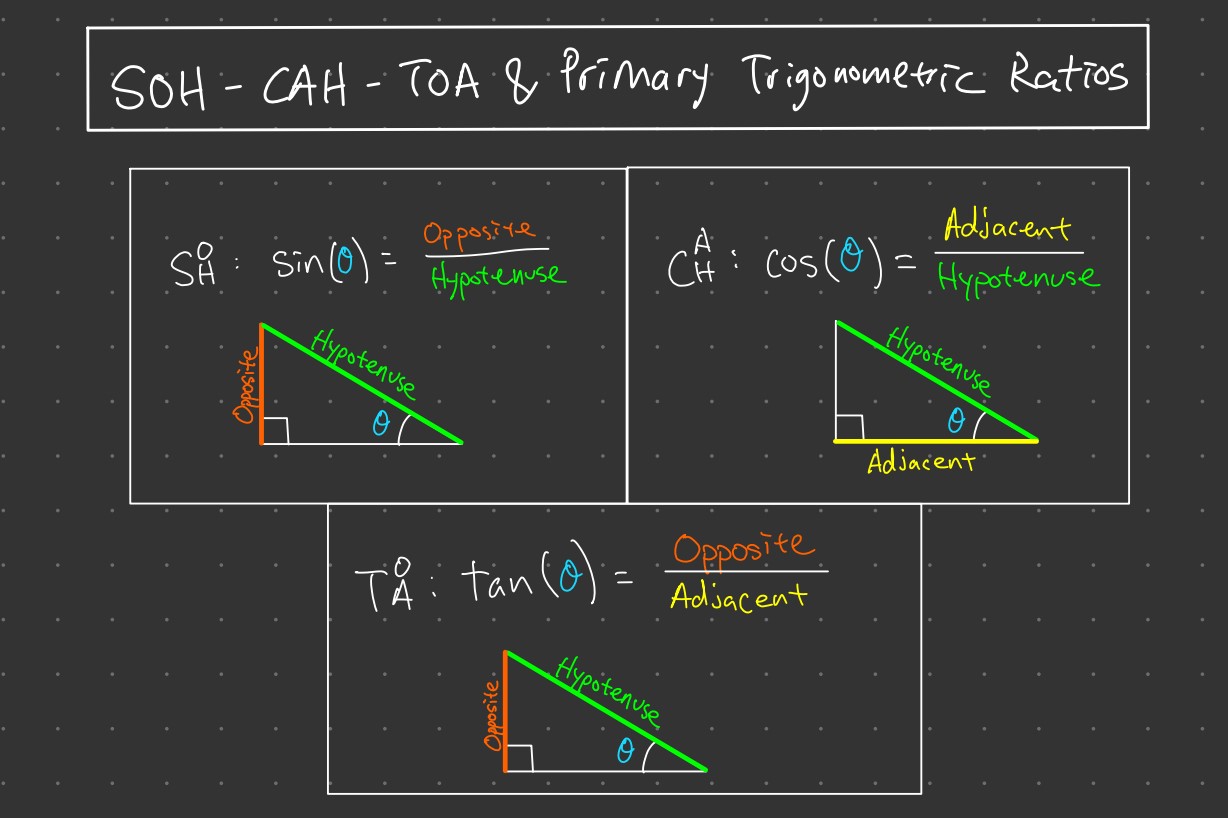
Sine ( $\sin$ )

Imagine you are on a playground, and you want to swing back and forth. The Sine ratio helps you understand how high you go with each swing.

Definition: The Sine of an angle in a right-angled triangle is the ratio of the length of the side opposite the angle to the hypotenuse.
Formula: $\sin(\theta) = \frac{opposite}{hypotenuse}$

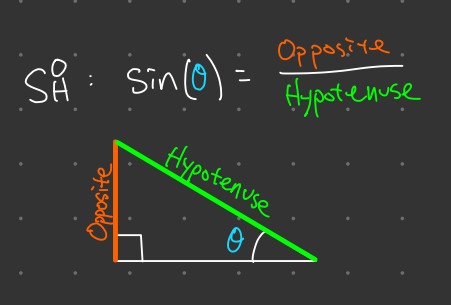
Cosine ( $\cos$ )

Now, picture yourself sliding down a slide. The Cosine ratio explains how far you slide along the ground.

Definition: The Cosine of an angle in a right-angled triangle is the ratio of the length of the adjacent side to the hypotenuse.
Formula: $\cos(\theta) = \frac{adjacent}{hypotenuse}$

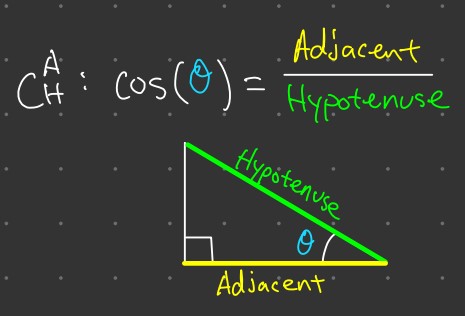
Tangent ( $\tan$ )

Lastly, let’s think about climbing up a ladder. The Tangent ratio helps you understand how steep the ladder is.

Definition: The Tangent of an angle in a right-angled triangle is the ratio of the length of the side opposite the angle to the adjacent side.
Formula: $\tan(\theta) = \frac{opposite}{adjacent}$

The Power of SOH CAH TOA

Applying the Ratios

Now that we’ve uncovered the secrets behind SOH CAH TOA, let’s see how we can apply these ratios to solve real-world problems.

Example 1: Finding a Missing Side

Imagine you have a right-angled triangle with an angle of 30 degrees, and the opposite side is 5 units. You want to find the hypotenuse.

Identify the Given and Unknown:
- Given: Angle $\theta = 30^\circ$ , Opposite side = 5 units.
- Unknown: Hypotenuse.
Choose the Right Ratio:
- Since we know the angle and the opposite side, we’ll use the Sine ratio.
- $\sin(30^\circ) = \frac{5}{\text{Hypotenuse}}$ .
Solve for the Unknown:
- $\text{Hypotenuse} = \frac{5}{\sin(30^\circ)}$ .
Calculate:
- $\text{Hypotenuse} = \frac{5}{0.5} = 10$ units.

So, the hypotenuse of the triangle is 10 units.

Example 2: Finding an Angle

Now, let’s say you have a triangle with a known adjacent side of 8 units and a hypotenuse of 10 units. You want to find the angle.

Identify the Given and Unknown:
- Given: Adjacent side = 8 units, Hypotenuse = 10 units.
- Unknown: Angle $\theta$ .
Choose the Right Ratio:
- Since we know the adjacent side and the hypotenuse, we’ll use the Cosine ratio.
- $\cos(\theta) = \frac{8}{10}$ .
Solve for the Unknown:
- $\theta = \cos^{-1}\left(\frac{8}{10}\right)$ .
Calculate:
- $\theta \approx \cos^{-1}(0.8) \approx 36.87^\circ$ .

So, the angle $\theta$ is approximately 36.87 degrees.

Mastering SOH CAH TOA

Tips and Tricks

Now that you’ve got the basics, let’s explore some tips to master SOH CAH TOA effortlessly:

Use the Right Ratio:
- Identify which sides and angles are known and choose the appropriate ratio.
Memorize the Acronym:
- Remembering SOH CAH TOA is your key to trigonometric success.
Practice with Real-world Examples:
- Apply SOH CAH TOA to solve problems involving angles and sides in various contexts.
Visualize the Triangles:
- Draw diagrams to visualize the triangles and make problem-solving more intuitive.

Conclusion

Congratulations! You’ve unlocked the magic of SOH CAH TOA. Trigonometry might seem challenging, but with these fundamental ratios, you’re well on your way to mastering IB Maths. Keep practicing, visualize the triangles, and soon you’ll be swinging through trigonometric problems with ease. If you still need help with SOH CAH TOA, we encourage you to reach out to our IB Math Tutor for help!

So, next time you encounter a triangle, remember the power of SOH CAH TOA – your ultimate toolkit for unraveling the mysteries of angles and sides. Happy learning!