As you delve deeper into your IB Math journey, you’ll come across concepts such as domain and range, and inverse functions. These concepts play a crucial role in understanding the behavior of functions and their properties. In this article, we’ll explore these concepts in detail and provide you with a comprehensive understanding of how they work.
Understanding the Domain of a Function
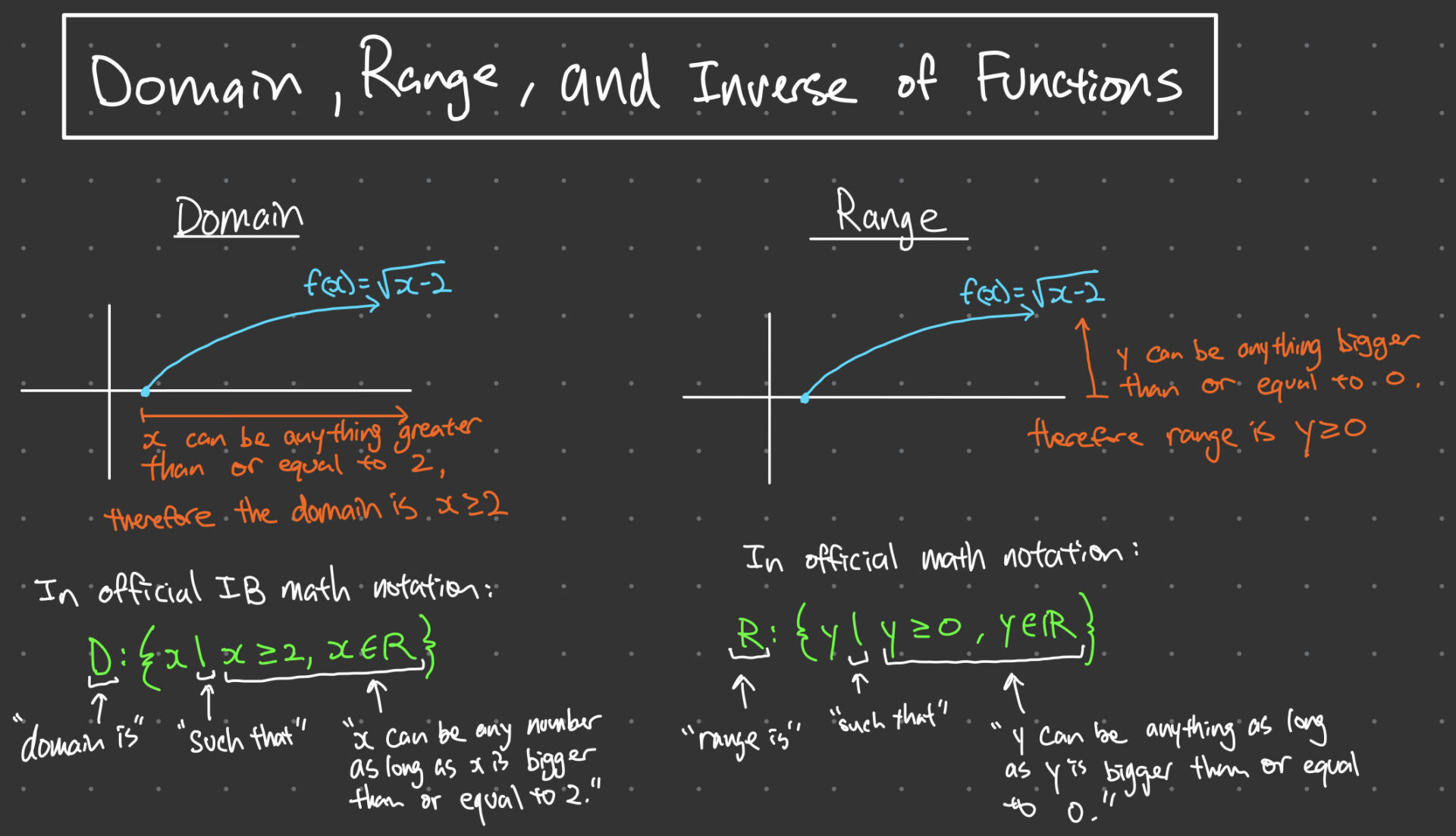
The domain of a function is the set of all possible input values for which the function is defined. In simpler terms, it refers to the set of all values that we can plug into the function to obtain an output, and in layman terms domain can thought as “what can x be”. The domain can be expressed in various forms, including interval notation, set notation, and inequality notation.
Let’s consider the following function:
f(x) = \sqrt{x-2}To determine the domain of this function, we need to consider the values of x that can be plugged into the function. However, the domain of this function is restricted because the square root function is undefined for negative values. Therefore, the domain of the function can be expressed as:
D_f = [2, \infty)This means that the function is defined for all values of x greater than or equal to 2.
Understanding the Range of a Function
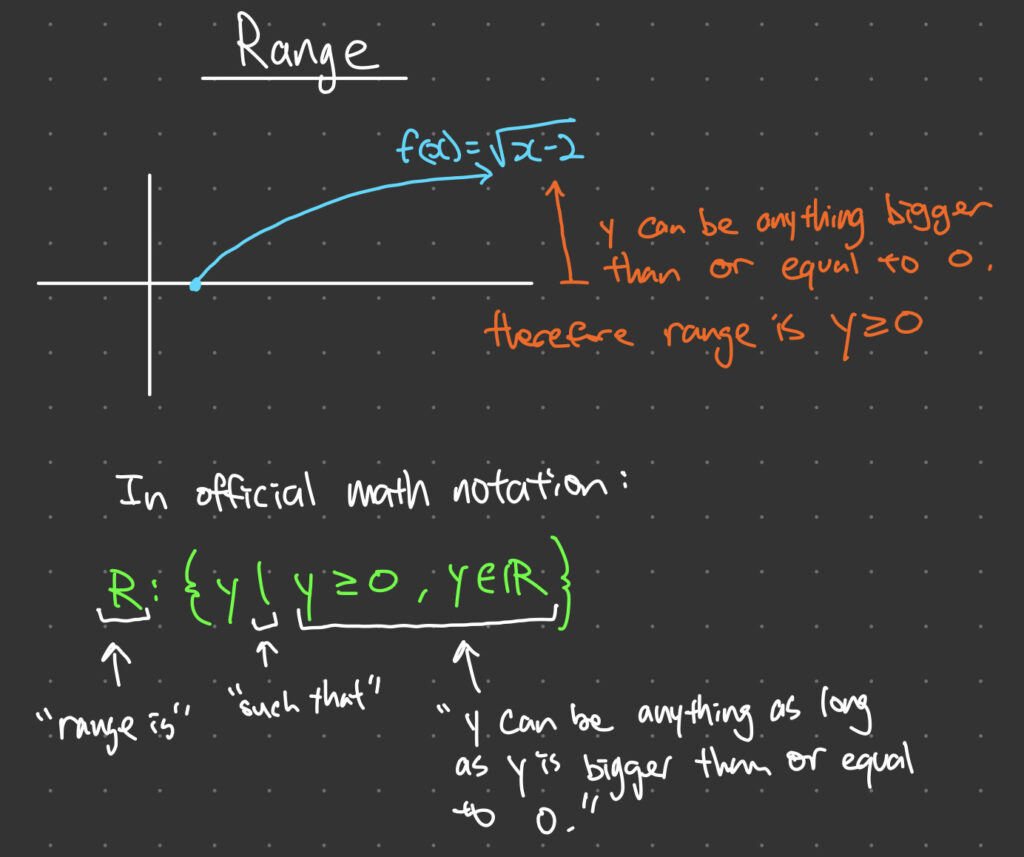
The range of a function refers to the set of all possible output values that the function can produce. In simpler terms, it refers to the set of all values that the function can take on, and in layman terms range can be thought as “what can y be”. The range can also be expressed in various forms, including interval notation, set notation, and inequality notation.
Let’s consider the same function as before:
f(x) = \sqrt{x-2}To determine the range of this function, we need to consider the values that the function can take on. Since the square root function can only output non-negative values, the range of the function can be expressed as:
R_f = [0, \infty)This means that the function can only produce values greater than or equal to 0.
Understanding Inverse Functions
An inverse function is a function that “undoes” the effect of another function. In simpler terms, it is a function that takes the output of a function as its input and produces the input of the function as its output. Inverse functions play a crucial role in many areas of mathematics and are essential in solving various mathematical problems.
To find the inverse of a function, we need to switch the roles of x and y and solve for y. Let’s consider the following function:
f(x) = 3x + 5To find the inverse of this function, we first switch the roles of x and y to obtain:
x = 3y + 5Next, we solve for y to obtain:
y = \frac{x – 5}{3}Therefore, the inverse of the function is:
f^{-1}(x) = \frac{x – 5}{3}It’s important to note that not all functions have an inverse. For a function to have an inverse, it must satisfy the horizontal line test, which means that no horizontal line intersects the graph of the function more than once.
Examples of Domain, Range, and Inverse Functions
Let’s consider the following function:
f(x) = x^2 – 4x + 3To determine the domain
of this function, we need to consider the values of x that can be plugged into the function. Since the function is a quadratic function, it is defined for all real values of x. Therefore, the domain of the function is:
D_f = (-\infty, \infty)To determine the range of the function, we need to consider the values that the function can take on. We can rewrite the function as:
f(x) = (x – 2)^2 – 1From this form, we can see that the minimum value of the function occurs when x = 2, and the value is -1. Therefore, the range of the function is:
R_f = [-1, \infty)To find the inverse of the function, we first switch the roles of x and y to obtain:
x = y^2 – 4y + 3Next, we complete the square to obtain:
x = (y – 2)^2 – 1Then, we solve for y to obtain:
y = 2 \pm \sqrt{x + 1}Therefore, the inverse of the function is:
f^{-1}(x) = 2 \pm \sqrt{x + 1}It’s important to note that since the original function is not one-to-one, we have two possible inverse functions.
Using Domain and Range to Determine Function Behavior
Understanding the domain and range of a function can also help us determine the behavior of the function. For example, let’s consider the function:
f(x) = \frac{1}{x – 1}The function is undefined when x = 1 since we cannot divide by zero. Therefore, the domain of the function is:
D_f = (-\infty, 1) \cup (1, \infty)To determine the behavior of the function as x approaches 1, we can use the limit notation. We can write:
\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = \pm \inftyThis means that as x approaches 1 from the left or the right, the function approaches positive or negative infinity, respectively. Therefore, we can say that the function has a vertical asymptote at x = 1.
Conclusion
Understanding the concepts of domain, range, and inverse functions is essential in IB Math, as it is the foundation for many other topics, such as calculus and trigonometry. Domain and range help us determine the possible input and output values of a function, while inverse functions allow us to find the input value given an output value. By understanding these concepts, we can also determine the behavior of a function, such as the presence of asymptotes.
In summary, here are the key takeaways from this article:
- The domain of a function is the set of all possible input values for which the function is defined.
- The range of a function is the set of all possible output values that the function can produce.
- To find the inverse of a function, we switch the roles of x and y and solve for y.
- Understanding the domain and range of a function can help us determine the behavior of the function, such as the presence of asymptotes.
- Not every function has an inverse, and a function can only have one inverse.
By applying these concepts, we can better understand and analyze functions in IB Math.
FAQ
No, a function can only have one domain. The domain is the set of all possible input values for which the function is defined.
Yes, a function can have an empty domain if it is undefined for all possible input values.
Yes, a function can have an empty range if it does not produce any output values.
No, not every function has an inverse. For a function to have an inverse, it must satisfy the horizontal line test.
No, a function can only have one inverse. If a function has multiple inverses, then it is not a function.