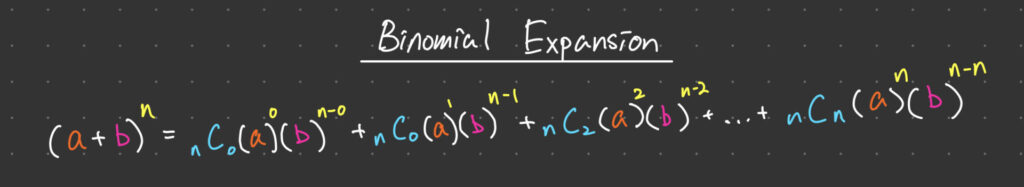If you’re studying for the International Baccalaureate (IB) Math exam, you may have come across the Binomial Theorem and Expansion. This concept is an essential tool in solving problems that involve polynomials and binomials. In this article, we’ll explore the Binomial Theorem and Expansion, and how to use them to solve problems in IB Math.
What is the Binomial Theorem?
The Binomial Theorem is a formula used to expand a binomial expression raised to a positive integer power. A binomial is an expression with two terms, such as (a + b). The Binomial Theorem provides a way to expand an expression of the form (a + b)^n, where n is a positive integer.
The Binomial Theorem can be expressed as follows:
(a+b)^n = \sum_{k=0}^{n} {n\choose k} a^{n-k} b^kWhere {n\choose k} is the binomial coefficient, defined as:
{n\choose k} = \frac{n!}{k!(n-k)!}The Binomial Theorem may look intimidating at first glance, but it’s a powerful tool that can simplify complex expressions. Let’s take a closer look at how to use the Binomial Theorem to expand a binomial.
Pascal’s Triangle – Coefficients of the Binomial Expansion
Pascal’s Triangle is a triangular array of numbers where each row represents the coefficients of the Binomial Expansion of (a+b)^n for a specific value of n. The first row of Pascal’s Triangle contains the number 1, and each subsequent row is formed by adding the two adjacent numbers in the row above.
The numbers in Pascal’s Triangle have many interesting properties and applications in mathematics. For instance, the sum of the numbers in the nth row of Pascal’s Triangle is equal to 2^n, and the nth diagonal of Pascal’s Triangle contains the numbers of the Fibonacci sequence. Moreover, the rows of Pascal’s Triangle correspond to the coefficients of the powers of (a+b)^n in the Binomial Expansion, which is central to the Binomial Theorem.
How to Expand a Binomial Using the Binomial Theorem
Suppose we want to expand the expression (a + b)^3 using the Binomial Theorem. We can begin by identifying the values of n, a, and b:
- n = 3 (the power to which the binomial is raised)
- a = a (the first term in the binomial)
- b = b (the second term in the binomial)
We can then use the Binomial Theorem to expand the expression:
(a+b)^3 = \sum_{k=0}^{3} {3\choose k} a^{3-k} b^k = {3\choose 0} a^3 b^0 + {3\choose 1} a^2 b^1 + {3\choose 2} a^1 b^2 + {3\choose 3} a^0 b^3 = a^3 + 3a^2b + 3ab^2 + b^3So, we have expanded the expression (a + b)^3 using the Binomial Theorem. As you can see, the Binomial Theorem can simplify complex expressions and make them more manageable.
Applications of the Binomial Theorem
The Binomial Theorem has many applications in mathematics, science, and engineering. Here are some examples:
- Probability theory: The Binomial Theorem can be used to calculate the probability of a specific number of successes in a sequence of independent events.
- Combinatorics: The Binomial Theorem is used in combinatorics to calculate the number of ways to choose a subset of elements from a set.
- Engineering: The Binomial Theorem is used in engineering to calculate the power series expansion of functions.
Common mistakes when using Binomial Theorem and Expansion
Some common mistakes when using the Binomial Theorem and Expansion include:
- Not simplifying the expression before applying the formula
- Using the formula incorrectly
- Forgetting to include negative and fractional exponents in Binomial Expansion
- Using the wrong values for n, a, and b
To avoid these mistakes, it’s important to carefully follow the steps outlined in this article and practice solving problems using the Binomial Theorem and Expansion.
Conclusion
In summary, the Binomial Theorem and Expansion are powerful tools for solving problems that involve polynomials and binomials. The Binomial Theorem allows us to expand a binomial expression raised to a positive integer power, while Binomial Expansion allows us to expand a binomial expression raised to any real number, including fractions and negative numbers.
These concepts have many applications in mathematics, science, and engineering, and can simplify complex expressions, making them more manageable. By understanding the Binomial Theorem and Expansion, you can solve a wide range of problems in IB Math and beyond.
FAQ
A binomial is an expression with two terms, such as (a + b).
The Binomial Theorem is a formula used to expand a binomial expression raised to a positive integer power.
The formula for the Binomial Theorem is:
(a+b)^n = \sum_{k=0}^{n} {n\choose k} a^{n-k} b^kThe binomial coefficient is a number that represents the number of ways to choose k objects from a set of n objects. It is denoted by {n\choose k} and is defined as:
{n\choose k} = \frac{n!}{k!(n-k)!}