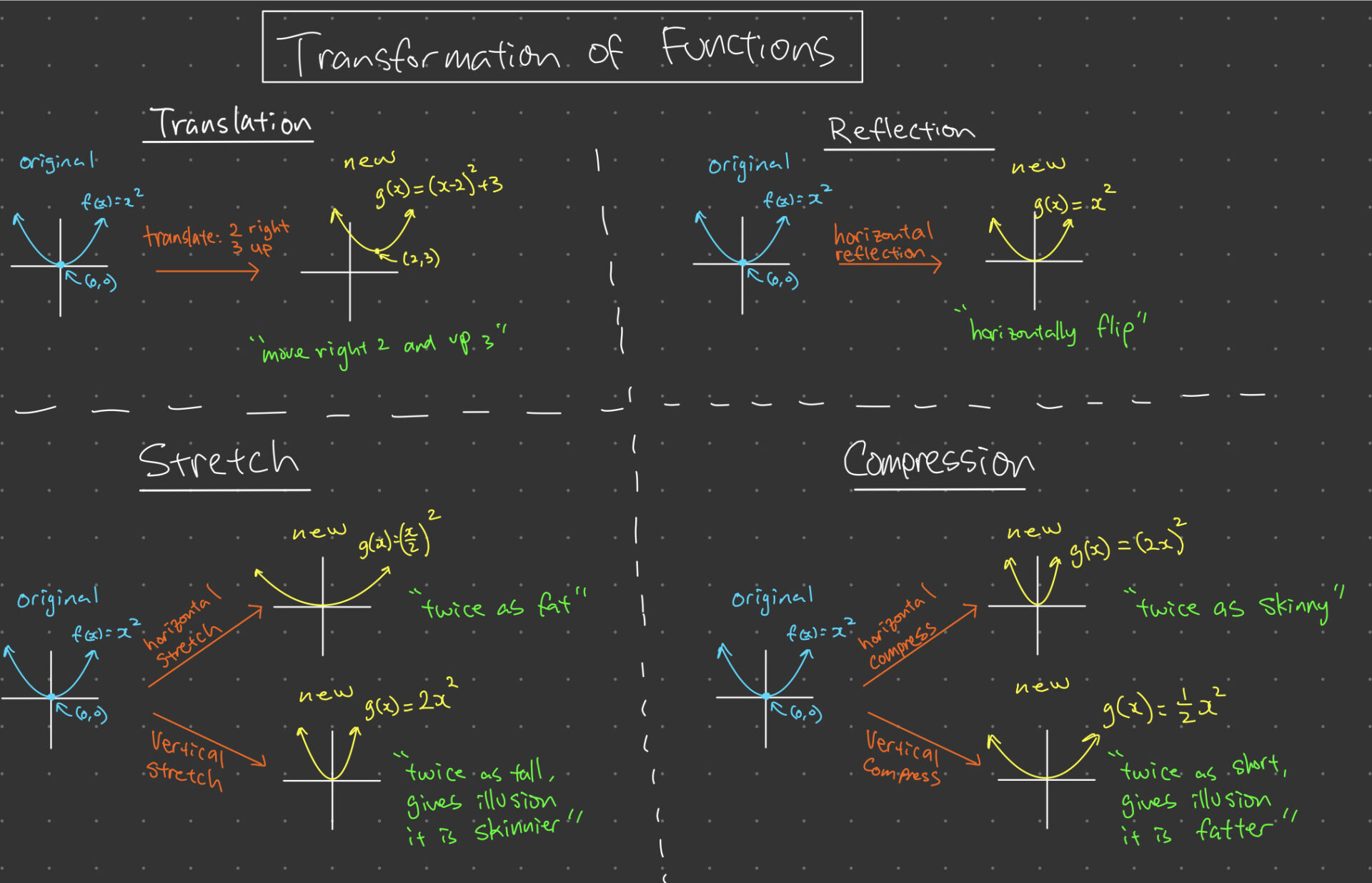
Transformation of Functions is a crucial topic in IB Math that deals with how to transform a function’s graph by changing its domain, range, and position on the Cartesian plane. This topic is essential for understanding the properties of different functions and how to manipulate them. In this article, we will discuss the different types of transformations of functions and their applications.
What is a Function?
Before we dive into the topic of Transformation of Functions, it is essential to understand what a function is. A function is a rule that maps each element from one set, called the domain, to exactly one element in another set, called the range. In other words, a function is a relation between two sets that assigns a unique output value to each input value.
For example, consider the function f(x) = x^2 Here, the domain is all real numbers, and the range is all non-negative real numbers. For each input value of x, the function outputs its square. Therefore, f(2) = 4, f(3) = 9, and so on.
What are Transformations of Functions?
Transformations of Functions refer to changes made to the graph of a function by modifying its equation. The resulting function is a transformation of the original function. These transformations can change the position, shape, and size of the function’s graph. The main types of transformations include:
- Translation
- Reflection
- Scaling
- Stretching
- Compression
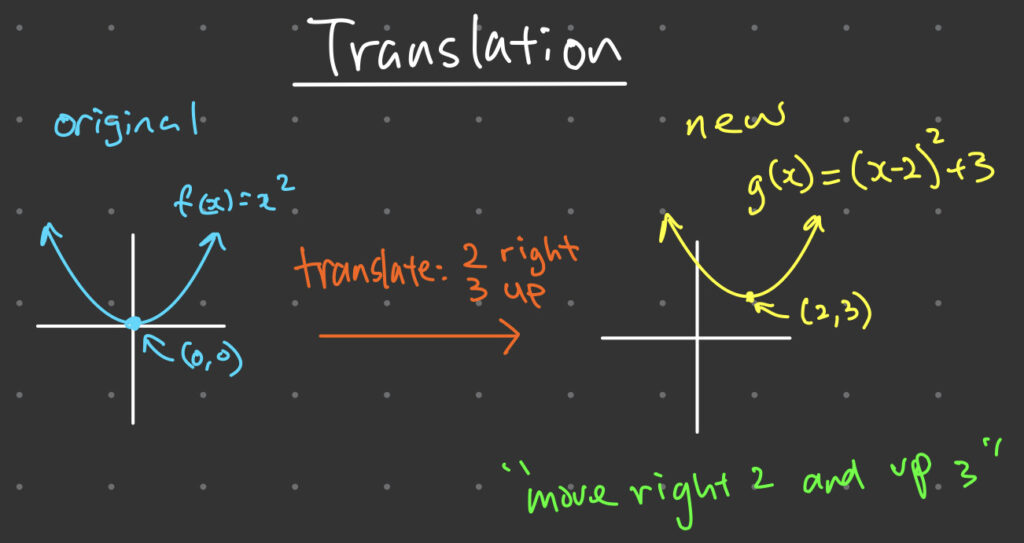
1. Transformation of Functions via Translation
Translation of a function is the process of moving its graph up, down, left or right without changing its shape or size. This transformation is achieved by adding or subtracting constants to the function.
For example, consider the function f(x) = x^2 To translate this function two units to the right and three units up, we modify the equation to become g(x) = (x-2)^2 + 3 This equation is obtained by subtracting 2 from x to move the graph two units to the right and adding 3 to f(x) to move the graph three units up.
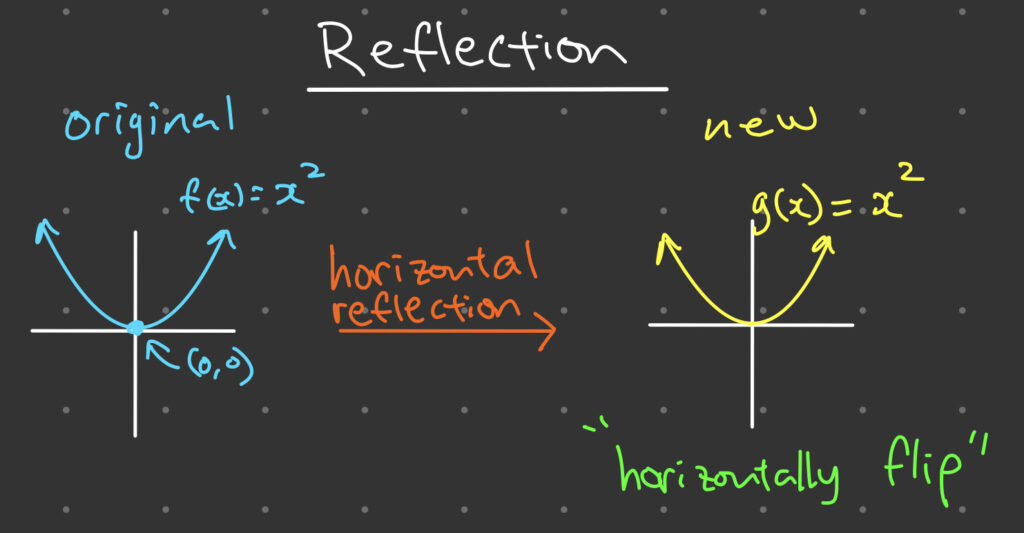
2. Transforming a Functions via Reflection
Reflection of a function is the process of flipping its graph across the x-axis or the y-axis. Reflection across the x-axis is achieved by multiplying the function by -1, while reflection across the y-axis is achieved by replacing x with -x in the function.
For example, consider the function f(x) = x^2 To reflect this function across the y-axis, we modify the equation to become g(x) = (-x)^2 = x^2 This equation is obtained by replacing x with -x in f(x), which gives the same output as f(x) for all input values of x.
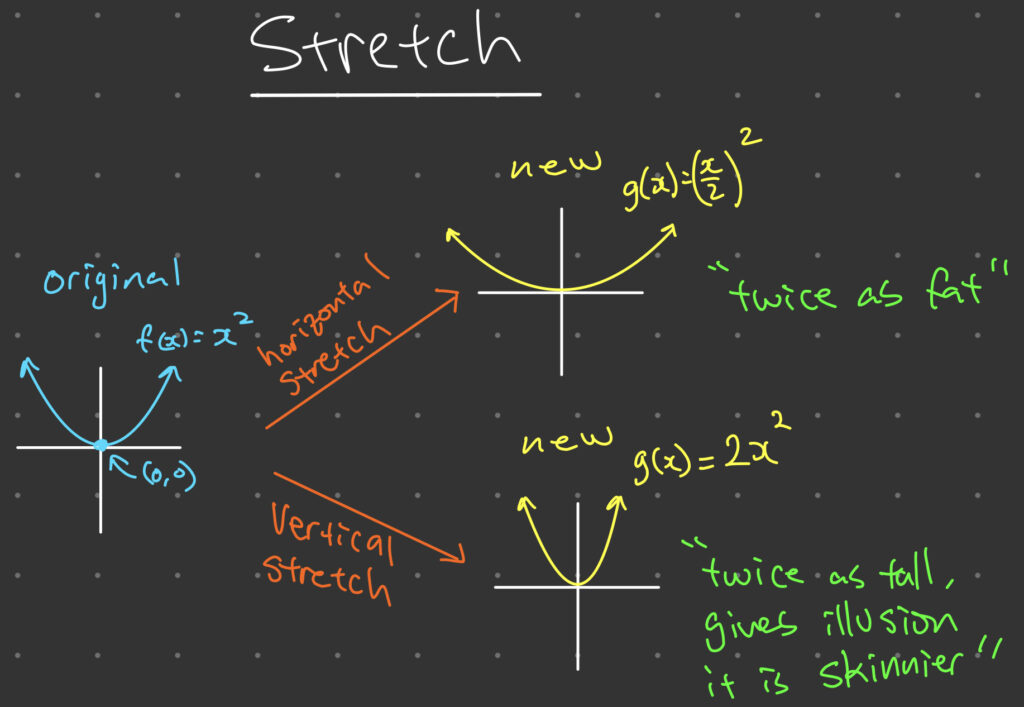
3. Transformation of Functions by Stretch
Stretching of a function is the process of changing the shape of its graph by expanding or compressing it in the vertical or horizontal direction. This transformation is achieved by multiplying or dividing the input variable by a constant.
There are two types of stretching: horizontal stretching and vertical stretching. A horizontal stretching or compression changes the function’s shape by changing the spacing between its input values. On the other hand, a vertical stretching or compression changes the function’s shape by changing the spacing between its output values.
For example, consider the function f(x) = x^2 To stretch this function horizontally by a factor of 2, we modify the equation to become g(x) = (\frac{x}{2})^2 This equation is obtained by dividing x by 2, which compresses the graph horizontally by a factor of 2. To stretch the function vertically by a factor of 2, we modify the equation to become h(x) = 2x^2 This equation is obtained by multiplying f(x) by 2, which stretches the graph vertically by a factor of 2.
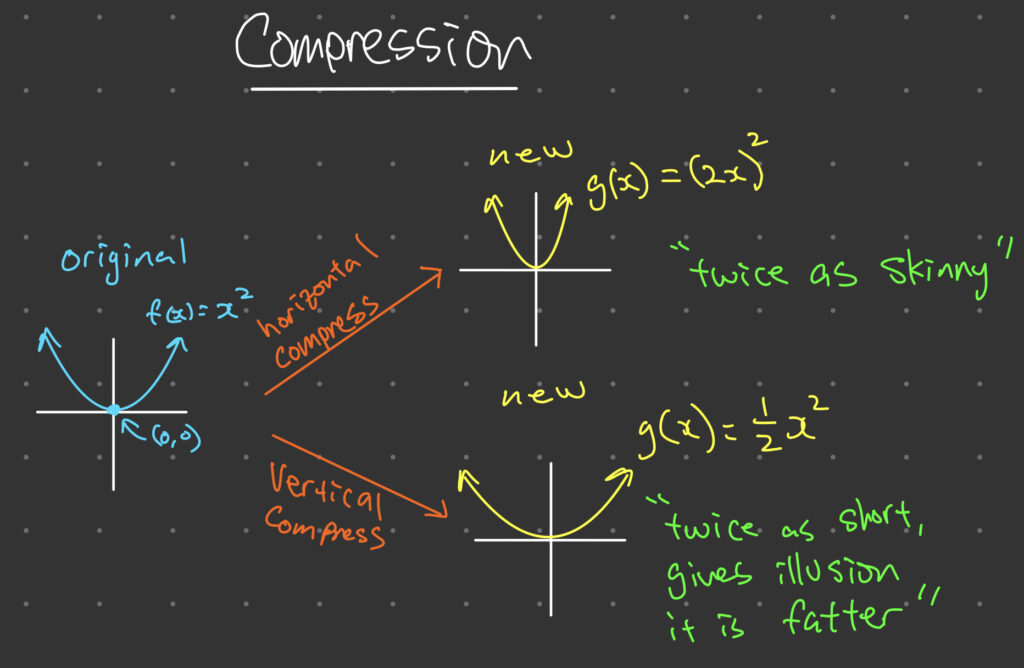
4. Function Transformations by Compression
Compression of a function is the process of squeezing its graph horizontally or vertically without changing its shape or position. This transformation is achieved by multiplying the function by the factor for vertical compression, or multiplying x with the reciprocal of the factor for horizontal compression.
For example, consider the function f(x) = x^2 To compress this function horizontally by a factor of 1/2, we modify the equation to become g(x) = (2x)^2 This equation is obtained by replacing x with 2x, which compresses the graph horizontally by a factor of 1/2. To compress the function vertically by a factor of 1/2, we modify the equation to become h(x) = \frac{1}{2}x^2 This equation is obtained multiplying the entire function by the compression factor, which compresses the graph vertically by a factor of 1/2.
Applications of Transformation of Functions
The transformation of functions is used in various fields, including physics, engineering, economics, and computer science. Some of the applications of transformation of functions include:
In physics, the transformation of functions is used to model physical phenomena such as motion, waves, and energy.
In economics, the transformation of functions is used to analyze and predict market trends and consumer behavior.
In computer science, the transformation of functions is used to manipulate digital images, sounds, and videos.
In engineering, the transformation of functions is used to design and optimize structures, machines, and systems.
Conclusion
Transformation of Functions is a crucial topic in IB Math that deals with how to transform a function’s graph by changing its domain, range, and position on the Cartesian plane. In this article, we discussed the different types of transformations of functions, including translation, reflection, scaling, stretching, and compression. We also discussed their applications in various fields such as physics, economics, computer science, and engineering.
FAQ
Transformation of functions is used in various fields, including physics, engineering, economics, and computer science. It is used to model physical phenomena, analyze and predict market trends and consumer behavior, manipulate digital images, sounds, and videos, and design and optimize structures, machines, and systems.
Yes, a function can be both translated and scaled at the same time. For example, the function f(x) = x^2 can be translated left by 2 units and stretched vertically by a factor of 3 to become g(x) = 3(x+2)^2
Yes, a function can be reflected twice. For example, the function f(x) = x^2 can be reflected first in the x-axis to become g(x) = -x^2 and then in the y-axis to become h(x) = x^2
A translation is a type of transformation that shifts a function’s graph horizontally or vertically without changing its shape or orientation. A transformation, on the other hand, is a broader term that encompasses all the different types of changes that can be made to a function’s graph, including translations, reflections, stretchings, and compressions.