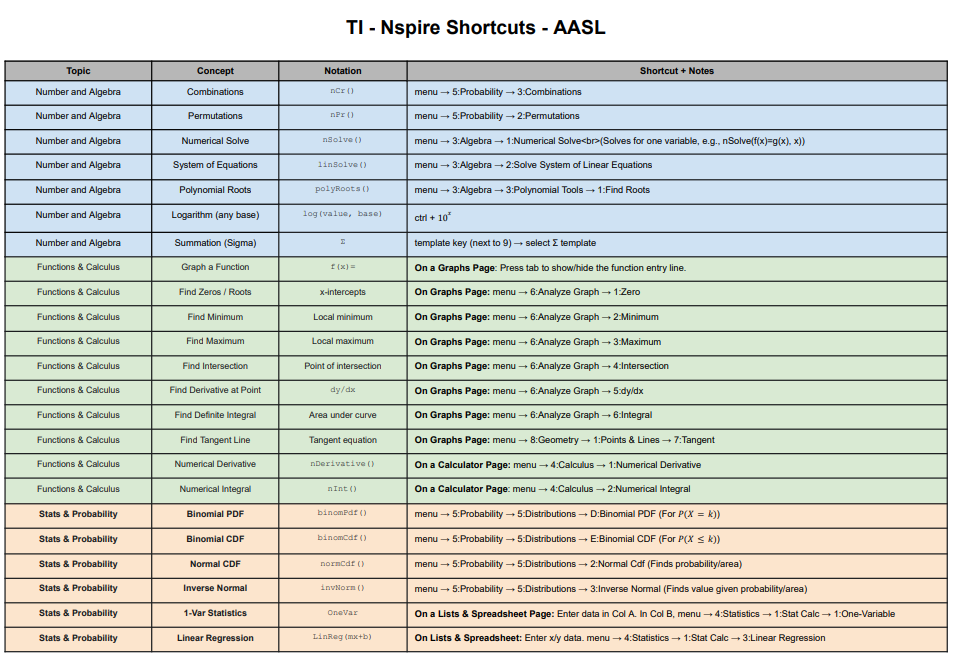
As a student of IB Math, you may have come across the concept of Sigma Notation. Sigma Notation is a concise way to represent the sum of a sequence of numbers. It is commonly used in mathematics and computer science to represent large sets of numbers, such as sums, products, and integrals. In this article, we will explore what Sigma Notation is, how to use it, and its applications in different areas of mathematics. This article serves as additional notes to the following video. You should first watch the video and then read the notes to see if you understand all the concepts.
What is Sigma Notation?
Sigma Notation is a mathematical notation that uses the Greek letter sigma (Σ) to represent a sum of a sequence of numbers. The sum is written as follows:
\sum_{i=m}^n a_i
In this notation, “i” represents the index of the sequence, “m” represents the starting value of “i,” “n” represents the ending value of “i,” and “a_i” represents the value of the “i-th” term in the sequence.
For example, the sum of the first five natural numbers can be represented as:
\sum_{i=1}^5 i
This can be read as “the sum from i equals 1 to i equals 5 of i.”
The result of the above sum can be calculated as:
\sum_{i=1}^5 i = 1 + 2 + 3 + 4 + 5 = 15
How to Use Sigma Notation?
Sigma Notation can be used to represent different types of sequences, such as arithmetic and geometric sequences. To use Sigma Notation, you need to follow these steps:
- Determine the starting and ending values of the sequence.
- Determine the general formula for the “i-th” term of the sequence.
- Write the general formula for the sum using Sigma Notation.
- Evaluate the sum by replacing the variables with the starting and ending values of the sequence.
For example, the sum of the first ten even numbers can be represented as:
\sum_{i=1}^{10} 2i
This can be read as “the sum from i equals 1 to i equals 10 of 2i.”
The result of the above sum can be calculated as:
\sum_{i=1}^{10} 2i = 2(1) + 2(2) + … + 2(10) = 110
Applications of Sigma Notation (Not Really Tested in IB)
Sigma Notation is widely used in mathematics, science, and engineering to represent the sum of a sequence of numbers. Here are some examples of how Sigma Notation is used in different areas of mathematics:
Calculus
In calculus, Sigma Notation is used to represent the sum of infinitesimal elements. For example, the area under a curve can be approximated by dividing the curve into small segments and adding up the areas of the segments. This can be represented using Sigma Notation as follows:
\sum_{i=1}^{n} f(x_i) \Delta x
where “f(x_i)” represents the value of the function at the “i-th” segment, and “Δx” represents the width of the segment.
Number Theory
In number theory, Sigma Notation is used to represent the sum of divisors of a number. For example, the sum of divisors of the number 12 can be represented as:
\sum_{d|12} d = 1 + 2 + 3 + 4 + 6 + 12
In this notation, “d” represents a divisor of 12. The symbol “|12” means “divides 12.”
Statistics
In statistics, Sigma Notation is used to represent the sum of a data set. For example, the sample mean of a data set can be represented using Sigma Notation as follows:
\frac{1}{n} \sum_{i=1}^{n} x_i
where “x_i” represents the “i-th” element of the data set and “n” represents the number of elements in the data set.
Tips for Using Sigma Notation
Here are some tips for using Sigma Notation effectively:
- Understand the notation. Make sure you understand the symbols and the meaning of the notation before attempting to use it.
- Check the limits of the sum. Make sure you understand the starting and ending values of the index “i.”
- Simplify the formula. Try to simplify the formula by factoring out common terms or using algebraic identities.
- Be careful with negative numbers. Make sure you include the negative sign inside the parentheses when working with negative numbers.
- Use parentheses. Use parentheses to avoid confusion when working with complex formulas.
Conclusion
Sigma Notation is a useful tool for representing the sum of a sequence of numbers. It is widely used in mathematics, science, and engineering to represent different types of sequences, such as arithmetic and geometric sequences. Understanding Sigma Notation is essential for IB Math students and anyone who needs to work with sums in their studies or work.
FAQ
Q1. What is the difference between Sigma Notation and Pi Notation?
Sigma Notation represents the sum of a sequence of numbers, while Pi Notation represents the product of a sequence of numbers. Pi Notation uses the Greek letter pi (Π) instead of sigma (Σ) and has a similar format to Sigma Notation.
Q2. Can Sigma Notation be used to represent infinite series?
Yes, Sigma Notation can be used to represent infinite series. In this case, the ending value “n” is replaced by infinity (∞).
Q3. What is the purpose of Sigma Notation in calculus?
Sigma Notation is used in calculus to represent the sum of infinitesimal elements, such as the area under a curve or the volume of a solid. It is a useful tool for approximating integrals and solving other calculus problems.
Q4. Can Sigma Notation be used to represent complex numbers?
Yes, Sigma Notation can be used to represent complex numbers. In this case, the sequence of complex numbers is represented using a formula that involves the real and imaginary parts of the numbers.
Q5. Is Sigma Notation used in computer science?
Yes, Sigma Notation is used in computer science to represent sums and other types of sequences. It is a useful tool for writing algorithms and solving computational problems.