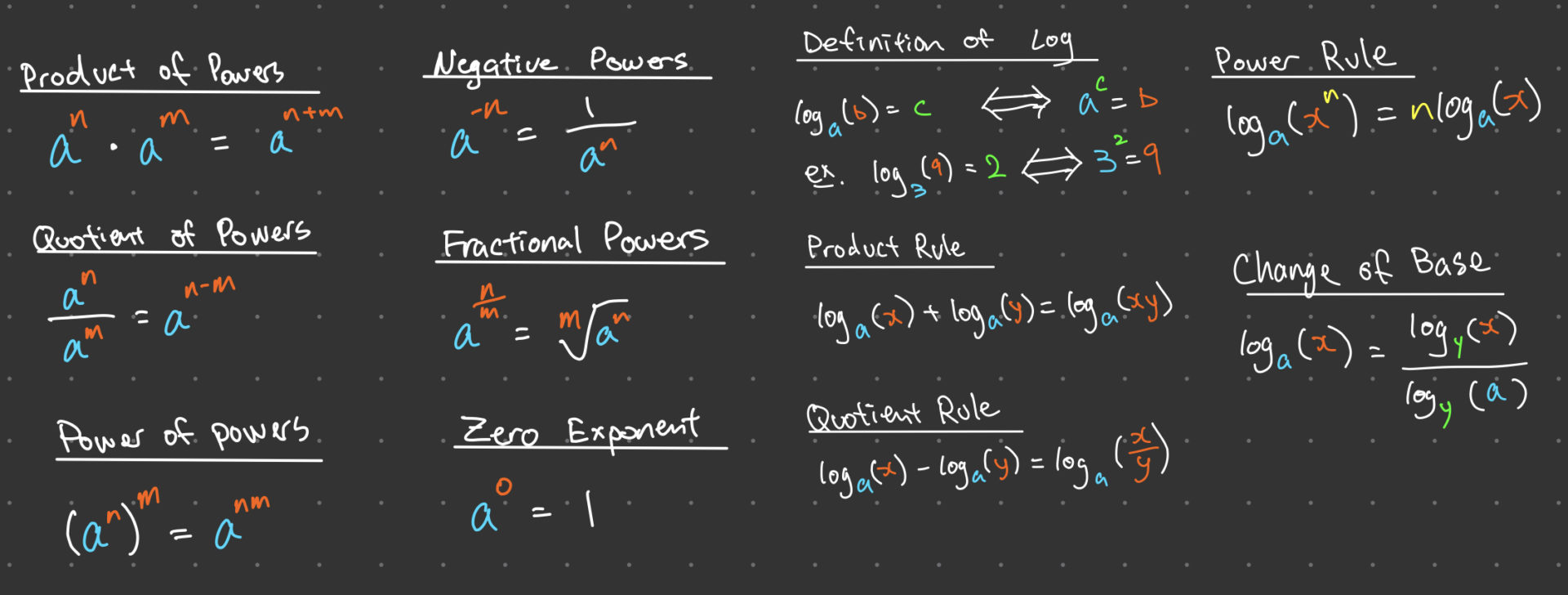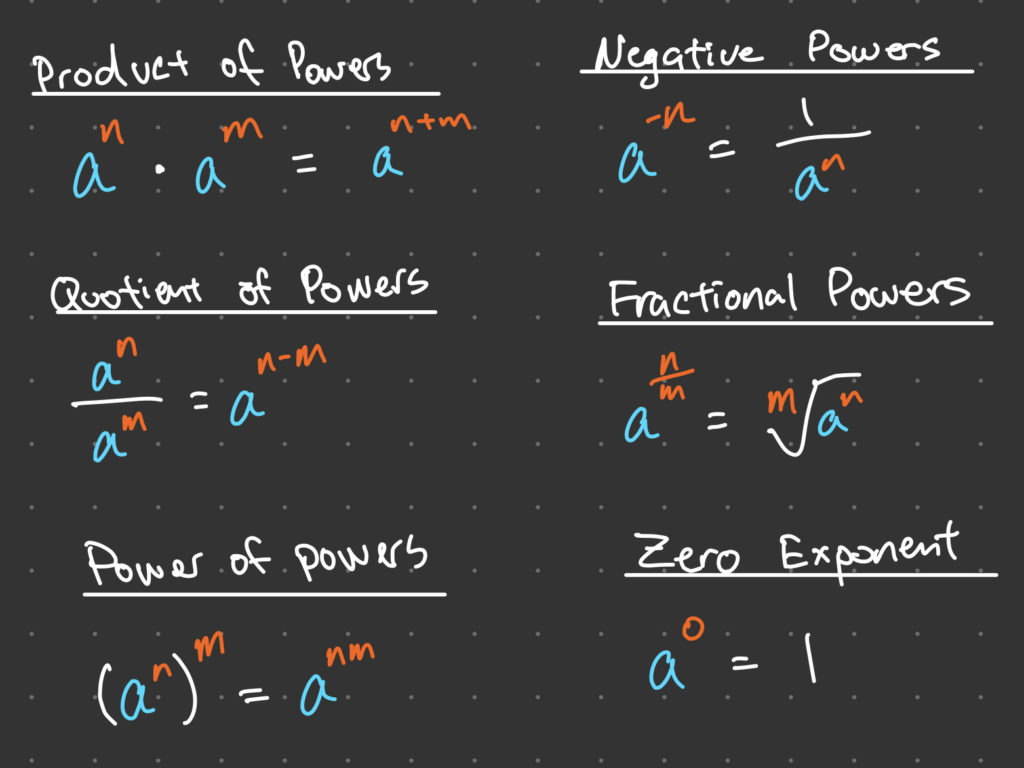IB Mathematics is an advanced-level course that covers a wide range of mathematical concepts, including exponents and logarithms. These concepts are fundamental to the study of mathematics and are used extensively in various fields of science, engineering, and economics. In this blog post, we will explore the laws of exponents and logarithms in detail and how they are used in various contexts.
Laws of Exponents
Exponents are a shorthand notation used to represent repeated multiplication of a number by itself. The general form of an exponent is written as follows:
a^n
where “a” is the base and “n” is the exponent. For example, 3^4 means three raised to the power of four, which is equal to 81. The laws of exponents are a set of rules that govern the behavior of exponents and are essential to simplify expressions involving exponents. The following are the six laws of exponents:
Exponent Law 1: Product of powers
The product of two exponential expressions with the same base is equal to the base raised to the sum of the exponents. This law can be written as:
a^n \cdot a^m = a^{n+m}
For example, 2^3 \cdot 2^4 = 2^{3+4} = 2^7.
Exponent Law 2: Quotient of powers
The quotient of two exponential expressions with the same base is equal to the base raised to the difference of the exponents. This law can be written as:
\frac{a^n}{a^m} = a^{n-m}
For example, \frac{5^4}{5^2} = 5^{4-2} = 5^2.
Exponent Law 3: Power of a power
An exponential expression raised to another exponent is equal to the base raised to the product of the exponents. This law can be written as:
\left(a^n\right)^m = a^{nm}
For example, \left(3^2\right)^3 = 3^{2\cdot3} = 3^6.
Exponent Law 4: Negative exponents
A negative number in the exponent can be rewritten as a reciprocal. This law can be written as:
a^{-n} = \frac{1}{a^n}
For example, 3^{-2} = \frac{1}{3^2}.
Exponent Law 5: Fractional exponent
When there is a fraction in the exponent position, the number can be written with a radical symbol. This law can be written as:
a^{\frac{n}{m}} = \sqrt[m]{a^n}
For example, 4^{\frac{2}{3}} = \sqrt[3]{4^2}.
Exponent Law 6: Zero exponent
Any base raised to the zero exponent is equal to one. This law can be written as:
a^0 = 1
For example, 5^0 = 1.
Laws of Logarithms
Logarithms are the inverse operations of exponentiation. The logarithm of a number “x” to a given base is the power to which the base must be raised to produce the number “x”. The general form of a logarithmic expression is written as follows:
\log_a{x} = y
where “a” is the base, “x” is the argument, and “y” is the exponent or logarithm. The laws of logarithms are a set of rules that govern the behavior of logarithms and are essential to simplify expressions involving logarithms. The following are the three laws of logarithms:
Log Law 1: Product rule
The logarithm of a product of two numbers is equal to the sum of the logarithms of the individual numbers. This law can be written as:
\log_a{(xy)} = \log_a{x} + \log_a{y}
For example, \log_{10}{(3\cdot 4)} = \log_{10}{3} + \log_{10}{4}.
Log Law 2: Quotient rule
The logarithm of a quotient of two numbers is equal to the difference of the logarithms of the individual numbers. This law can be written as:
\log_a{\left(\frac{x}{y}\right)} = \log_a{x} – \log_a{y}
For example, \log_{10}{\left(\frac{3}{4}\right)} = \log_{10}{3} – \log_{10}{4}.
Log Law 3: Power rule
The logarithm of a number raised to a power is equal to the product of the exponent and the logarithm of the number. This law can be written as:
\log_a{x^n} = n\log_a{x}
For example, \log_{10}{(2^3)} = 3\log_{10}{2}.
Applications of Exponents and Logarithms
Exponents and logarithms have numerous applications in mathematics and other fields. Some of the key applications are as follows:
1. Compound interest
The formula for calculating compound interest involves exponential functions. Compound interest is calculated using the following formula:
A = P\left(1 + \frac{r}{n}\right)^{nt}
where “A” is the final amount, “P” is the principal amount, “r” is the annual interest rate, “n” is the number of times interest is compounded per year, and “t” is the number of years. This formula involves exponential functions, and it can be simplified using the laws of exponents.
2. Population growth
The population growth rate of a country or region can be modeled using exponential functions. The growth rate is typically expressed as a percentage, and the formula for calculating population growth is as follows:
P(t) = P_0e^{rt}
where “P(t)” is the population at time “t”, “P0” is the initial population, “r” is the growth rate, and “e” is Euler’s number. This formula involves exponential functions, and it can be simplified using the laws of exponents.
3. Sound and light
The intensity of sound and light waves can be measured using logarithmic scales. The decibel (dB) scale is used to measure the intensity of sound, while the Bel (B) scale is used to measure the intensity of light. Both scales are logarithmic, and they allow us to measure a wide range of intensities.
4. pH Scale
The pH scale is used to measure the acidity or basicity of a solution. The pH scale is logarithmic, and it ranges from 0 to 14. A pH of 7 is considered neutral, while pH values below 7 indicate acidity, and pH values above 7 indicate basicity.
5. Signal processing
Signal processing is a branch of electrical engineering that deals with the analysis and manipulation of signals. Signal processing involves the use of Fourier transforms, which are based on exponential functions. Fourier transforms allow us to analyze signals in terms of their frequency components, and they are used in numerous applications, including audio and image processing.
6. Cryptography
Cryptography is the practice of secure communication in the presence of third parties. Cryptography involves the use of mathematical algorithms to encrypt and decrypt messages. Many encryption algorithms are based on exponential functions and logarithms, making them secure and difficult to crack.
FAQ
Q1: What is the difference between an exponent and a logarithm?
A: An exponent is a number that indicates the power to which a base must be raised, while a logarithm is the power to which a base must be raised to produce a given number. Exponents and logarithms are inverse operations of each other.
Q2: What is the purpose of the laws of exponents and logarithms?
A: The laws of exponents and logarithms are used to simplify expressions involving exponents and logarithms. These laws allow us to manipulate exponential and logarithmic expressions in a way that makes them easier to work with.
Q3: What are some applications of exponents and logarithms?
A: Exponents and logarithms have numerous applications in mathematics and other fields, including compound interest, population growth, sound and light, the pH scale, signal processing, and cryptography.
Q4: How can I simplify an expression involving exponents or logarithms?
A: To simplify an expression involving exponents, use the laws of exponents to combine like terms or separate factors. To simplify an expression involving logarithms, use the laws of logarithms to combine or separate terms.