Derivatives are an essential concept in IB Math calculus topic and have numerous applications in various fields such as engineering, physics, economics, and finance. The derivative of a function is a measure of how the function changes as its input changes. It is used to determine the slope of a curve at any point, find the rate of change of a quantity, and locate the maximum or minimum points of a function. In this blog post, we will explore the topic of local maximum, minimum, and point of inflection in derivatives. We will discuss what they mean, how to find them, and their applications. Please watch the video first and then read the article below to consolidate your understanding. Note that the examples used in the video are different to the ones used in this article.
Local Maximum and Minimum
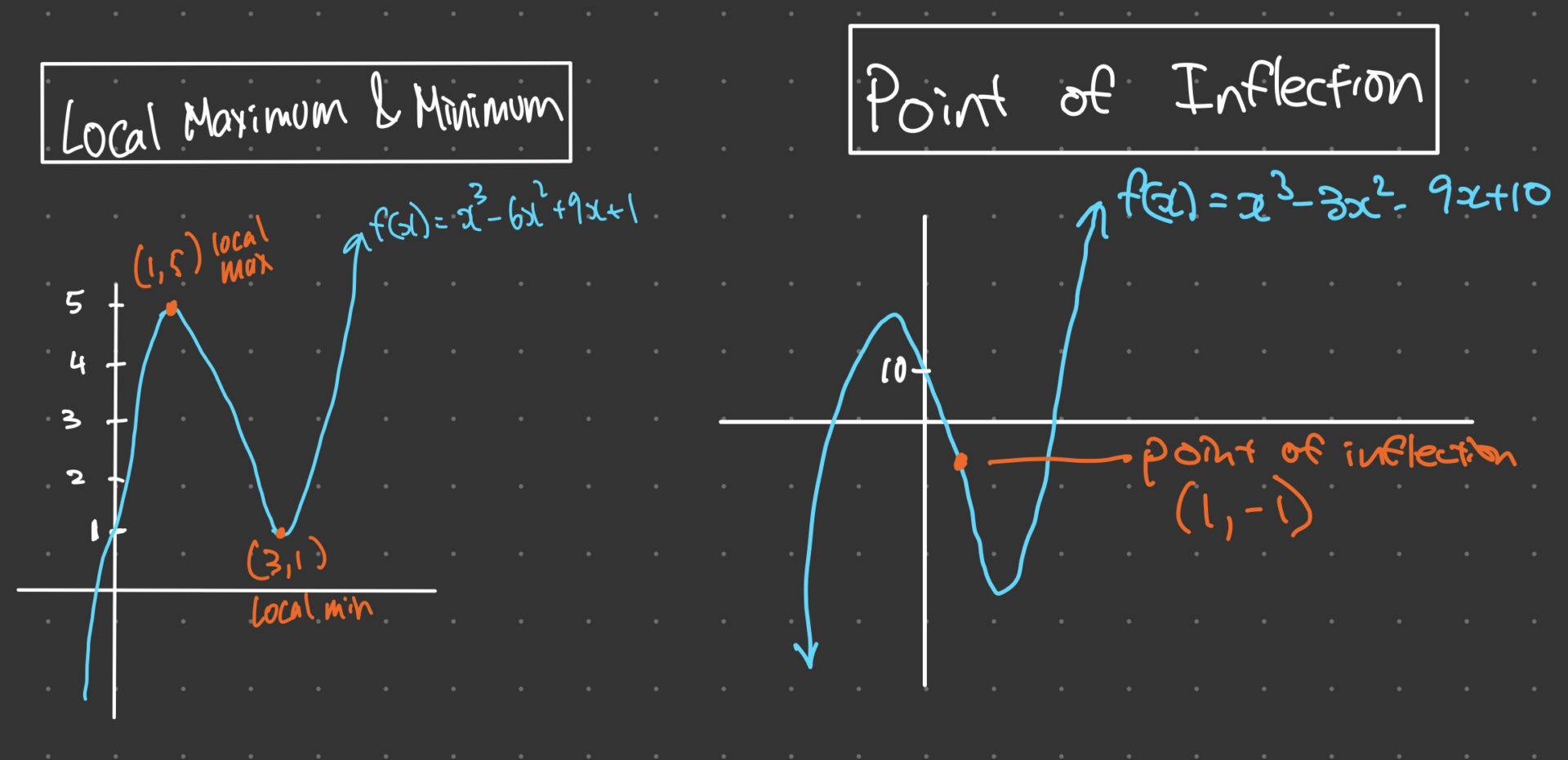
A local maximum or minimum is a point on a curve where the function reaches its highest or lowest value, respectively. It is called local because it is only a maximum or minimum within a certain range of values, not necessarily the absolute maximum or minimum of the entire function. For example, consider the function:
f(x) = x^3 – 6x^2 + 9x + 1
We can use the derivative of the function, f'(x), to find the local maximum and minimum points. To do this, we need to find where the derivative equals zero or does not exist. These points are called critical points. We then evaluate the function at each critical point to determine if it is a local maximum or minimum.
To find the critical points of the function above, we first find the derivative:
f'(x) = 3x^2 – 12x + 9
We then set the derivative equal to zero and solve for x:
3x^2 – 12x + 9 = 0
Factorizing the equation, we get:
3(x-1)(x-3) = 0
Solving for x, we get two critical points, x=1 and x=3. To determine if these are local maximum or minimum points, we evaluate the function at each point:
f(1) = 5, \quad f(3) = 1
Therefore, x=1 is a local maximum point and x=3 is a local minimum point.
Point of Inflection
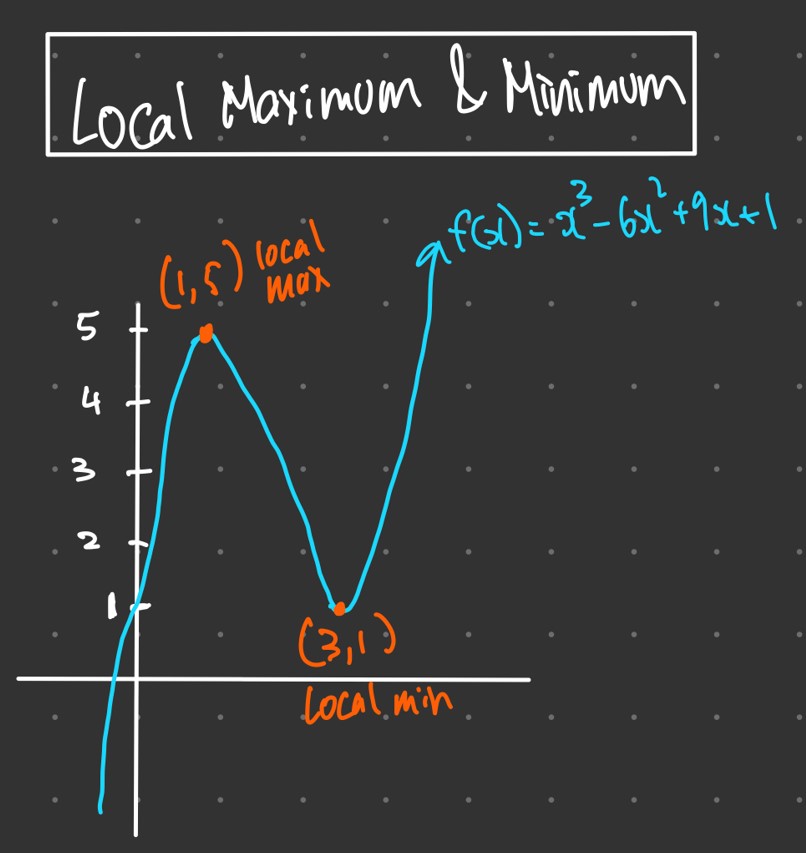
A point of inflection is a point on a curve where the concavity changes. In other words, it is a point where the second derivative of the function, f''(x), changes sign. At a point of inflection, the curve changes from being concave up to concave down or vice versa. For example, consider the function:
f(x) = x^3 – 3x^2 – 9x + 10
To find the point of inflection, we need to find where the second derivative equals zero or does not exist. These points are also called inflection points. We then evaluate the function at each inflection point to determine if it is a point of inflection.
To find the second derivative of the function above, we first find the first derivative:
f'(x) = 3x^2 – 6x – 9
We then find the second derivative:
f''(x) = 6x – 6
Setting the second derivative equal to zero, we get:
6x – 6 = 0
Solving for x, we get x=1. At x=1, the second derivative changes sign from negative to positive, indicating a point of inflection. To confirm this, we evaluate the function at x=1:
f(1) = -1
Therefore, x=1 is a point of inflection.
Applications
Local maximum, minimum, and point of inflection have numerous applications in various fields such as economics, physics, and engineering. In economics, they are used to determine the maximum or minimum profit or cost of a product. In physics, they are used to determine the maximum or minimum speed or acceleration of an object. In engineering, they are used to optimize the design of a structure or machine.
For example, in structural engineering, local maximum and minimum points are used to determine the maximum or minimum stress or strain of a material. Point of inflection is used to determine the bending moment and shear force of a beam. These values are essential in designing a structure that can withstand external forces and loads.
In finance, derivatives are used to model the behavior of financial assets such as stocks, bonds, and options. The local maximum and minimum points are used to determine the maximum or minimum value of an asset, while the point of inflection is used to determine the volatility of the asset.
Conclusion
Derivatives are an essential concept in calculus and have numerous applications in various fields such as economics, physics, and engineering. Local maximum, minimum, and point of inflection are important concepts in derivatives that are used to determine the maximum or minimum values of a function, the concavity of a curve, and the bending moment and shear force of a beam. By finding the critical points, inflection points, and evaluating the function at these points, we can determine if they are local maximum, minimum, or point of inflection. These values have numerous applications in various fields and are essential in optimizing the design of structures and machines, modeling financial assets, and determining the behavior of physical systems.
FAQ
What is a local maximum or minimum point?
A local maximum or minimum point is a point on a curve where the function reaches its highest or lowest value, respectively. It is called local because it is only a maximum or minimum within a certain range of values, not necessarily the absolute maximum or minimum of the entire function.
What is a point of inflection?
A point of inflection is a point on a curve where the concavity changes. In other words, it is a point where the second derivative of the function changes sign. At a point of inflection, the curve changes from being concave up to concave down or vice versa.
What are the applications of local maximum, minimum, and point of inflection?
Local maximum, minimum, and point of inflection have numerous applications in various fields such as economics, physics, and engineering. They are used to determine the maximum or minimum profit or cost of a product, the maximum or minimum speed or acceleration of an object, and to optimize the design of a structure or machine. In engineering, they are used to determine the maximum or minimum stress or strain of a material, and the bending moment and shear force of a beam. In finance, they are used to model the behavior of financial assets such as stocks, bonds, and options, and to determine the volatility of the asset.
How do you find the local maximum or minimum of a function?
To find the local maximum or minimum of a function, we need to find the critical points of the function, which are the points where the derivative of the function is equal to zero or does not exist. Once we find the critical points, we evaluate the function at these points to determine if they are local maximum or minimum. If the second derivative of the function is positive at the critical point, then it is a local minimum. If the second derivative of the function is negative at the critical point, then it is a local maximum.
How do you find the point of inflection of a function?
To find the point of inflection of a function, we need to find the points where the concavity of the curve changes. This occurs when the second derivative of the function changes sign. Once we find the points where the second derivative changes sign, we evaluate the function at these points to determine if they are point of inflection.